Estudio del Cálculo: La derivada y el problema de la recta tangente
Es realmente con el asentamiento de la derivada que nacen los verdaderos cimientos del cálculo moderno, anterior al descubrimiento de la derivada los estudios del cálculo se centraban en dar respuesta básicamente a cuatro problemas fundamentales: el problema de la recta tangente, el problema de la velocidad y la aceleración, el problema de los máximos y mínimos y el problema del área.
Fuente de imagen
Nota: la imagen ha sido copiada de wikimedia commons, el autor de la imagen es Olivier cleynen, el cual declara esta imagen al dominio público.
Existieron filósofos y matemáticos que trabajaron en dar solución a estos cuatros problemas, llegando a la conclusión que todo tenía respuestas en aproximar un punto arbitrario al punto tangencial mediante la teoría de límite (lo que conocemos hoy en día como derivada de una función). Sin embargo los trabajos más acertados fueron los de Isaac Newton y Gottfried Leibniz, que se traducen en la siguiente definición:
Definición de la recta tangente con pendiente m
Si f está definida en un intervalo abierto que contiene a c y además existe el límite, implica que:
Entonces, la recta que pasa por (c, f(c)) y cuenta con una pendiente m es la recta tangente a la gráfica de f en el punto (c, f(c)).
Cita textual: Libro de cálculo. Volumen I. Autor: Larson y Hostetler. Sección 2.1. Pag:97
La forma de encontrar la recta tangente con pendiente m en un punto dado por medio de la teoría de límite, da paso a la definición más aceptada que hoy en día conocemos de la derivada, y es que cuando se descubrió la derivada se llegó a un punto crucial en el cálculo infinitesimal, ya que con el límite utilizado para definir la pendiente de una recta también se utiliza para definir una de las dos operaciones fundamentales del cálculo: la derivación. La derivada de f en x viene dada por:
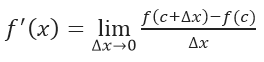
Para esta definición hay que tener presente que siempre que el límite exista hace que la función sea derivable, si el límite no existe la función es discontinua y no derivable.
Fuente de imagen
Nota: la imagen ha sido copiada de wikimedia commons, el autor de la imagen es Olivier cleynen, el cual declara esta imagen al dominio público.
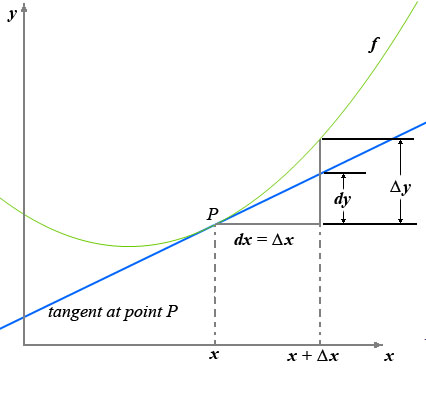
Fuente de imagen
Nota: la imagen ha sido copiada de wikimedia commons, el autor de la imagen es Goldencako. Este archivo está bajo la licencia Creative Commons Attribution-Share Alike 3.0 Unported.Sujeto a renuncias.
Ejemplo de cálculo de derivada de una función aplicando la definición de derivada
Calcular la derivada de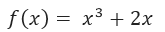 
Lo primero sería plantearnos la definición de la derivada:
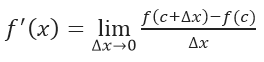
En este caso donde esté presente la variable x se sustituye por x+∆x y que c= x, esto implica que:
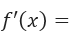
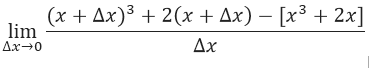
Una vez sustituido x por x + ∆x y f(x) por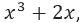 
tenemos que resolver el producto notable 
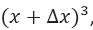hay que resolver las multiplicaciones de 
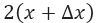y 
aplicando la propiedad distributiva, entonces nos quedaría de la siguiente manera:
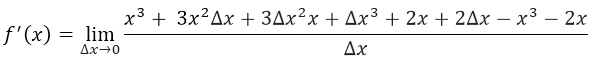
Realizando la suma algebraica de los términos del numerador, nos quedaría lo siguiente:
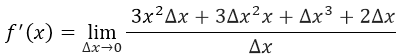
Es conveniente sacar factor común ∆x en el numerador, para de esta manera poder simplificar con el ∆x del denominador, lo que implica que:
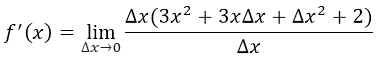
Se cancela el ∆x del numerador y denominador, y nos quedaría la siguiente expresión:
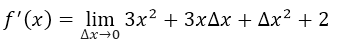
Si hacemos tender el límite de la función cuando ∆x→0, tenemos que sustituir ∆x por cero, por lo tanto:
Con lo que podemos concluir que la derivada de la función, es decir f'(x) es igual a:
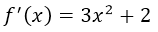
Conclusiones y lecciones aprendidas
El arduo trabajo de Leibniz y Newton por encontrar la solución a los problemas de la recta tangente y el problema de la aceleración y la velocidad fue concluyente para llegar a descubrir lo que hoy en día conocemos como derivada de una función.
El trabajo matemático en el cálculo infinitesimal no acabó en plantear la derivada como definición, sino que evolucionó con demostraciones hasta conseguir una serie de reglas básicas de derivación con las que hoy en día se hace mucho más fácil el trabajo de derivar funciones reales, a la vez esta evolución permitió a ciertas áreas de la ingeniería y la ciencia poder encontrar aplicaciones prácticas con la resolución de derivadas en términos de fenómenos donde las variables cambian unas con respecto a otras.
En publicaciones que subiré posteriormente explicare los mecanismos que facilitan la resolución de derivadas de manera más explícita y fácil en comparación a las derivadas por definición, todo esto ocurre cuando se emplean las reglas básicas de derivación, las cuales se emplean con la intención de minimizar esfuerzos y que se entiendan más los procesos para derivar por tablas que por definición.
A juicio propio es conveniente que toda aquella persona que se inicie en el estudio de las derivadas, entienda que el proceso de derivar no es proceso mecanizado, en donde mediante con una serie de fórmulas se realizan una serie de pasos para encontrar la derivada de una función, es decir hay que estar consciente que cada vez que se resuelve la derivada de una función real lo que se está consiguiendo es el valor de la pendiente de la recta que es tangente a la función en un punto dado. De esta manera estaremos muy consciente de lo que estamos consiguiendo y no de memorizar pasos y mecanizar procedimientos.
Referencias bibliográficas consultadas
Cálculo con Geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición. Editorial Mc Graw Hill. Volumen I. México 2006.
El Cálculo. Autor: Louis Leithold. 7ma edición. Editorial Oxford. México 1998.
"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-spanol, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de steemit que deseen publicar utilizando esta etiqueta a no cometer plagio."
Gracias por el apoyo brindado. Saludos al equipo de cervantes