Calculer une intégrale - Math
Source
Dans cet article, nous allons aborder une opération mathématique appelée Intégrale. Dans un premier temps, nous reviendrons sur la définition d'une fonction ainsi que de la dérivé. Puis, nous aborderons les intégrales de Riemann. Enfin, nous terminerons avec une application pratique.
Rappels
Une fonction
Pour rappel, une fonction f d'un ensemble D (domaine de définition) vers un ensemble F (ensemble d'image) est une correspondance qui assigne à chaque élément x de D exactement un élément y de F.
Dérivée
La dérivée d'une fonction f, que nous noterons f', en un point x correspond à l'application d'un accroissement Δx où nous allons chercher la pente de la corde correspondant à ces deux points. Nous allons chercher cette pente en réduisant au maximum l'écart entre notre point et l'accroissement. Vous pouvez voir la visualisation ci-dessous de cela.
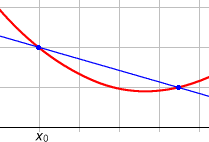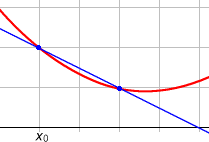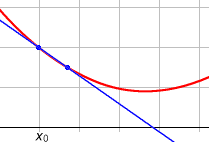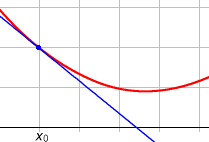
Source
Plus mathématiquement, nous aurons :
Nous avons aussi : y = f(x)
Ainsi, nous avons l'accroissement :
La différentielle dx de la variable indépendante x est dx = Δx
La différentielle dy de la variable dépendante y = dy = f'(x)Δx = f'(x)dx
Quand Δx ~ 0, alors Δy ~ dy
Ainsi : si y = f(x), alors :
Qu'est-ce qu'une intégrale ?
Une intégrale représentée par le signe ∫ peut être interpréter comme la somme de l'aire présent sous la courbe d'une fonction. Si nous prenons le schéma suivant, l'intégrale sur l'intervalle [a,b] de la fonction f correspond à l'aire coloriée en bleu.
Source
D'un point de vue mathématique, nous noterons :
Les intégrales de Riemann
Afin de pouvoir calculer l'aire en bleu, différentes méthodes existes. La méthode de Riemann est découpée notre aire en plein de rectangles. Ainsi, il nous suffit de faire la somme de l'ensemble des rectangles afin de pouvoir calculer l'aire. Nous pouvons visualiser cela avec le schéma ci-dessous.
Source
Ainsi, nous pouvons dire que pour un découpage, nous allons réaliser la somme de l'ensemble des rectangles. Ainsi, chaque rectangle a pour longueur la valeur de f en ce point et en largeur l'accroissement. Nous pouvons exprimer cela par :
Calculer une intégrale
- Soit f une fonction définie sur [a,b] et si F est une primitive de f, alors :
Pour rappel, la primitive correspond à l'opération inverse de la dérivée. Ainsi, F'(x) = f(x).
Application
Dans cet exemple, nous allons chercher à calculer l'intégrale de la fonction f(x) = x^2, sur l'intervalle [-1, 3].
Avant tout, nous allons chercher la primitive de f(x), qui correspond :
Ainsi, il ne nous reste plus qu'à réaliser le calcul :
Donc, l'aire se situant en dessous de la fonction x^2 sur l'intervalle [-1, 3] est égale à 28/3.
Mot de fin
Merci de votre temps de lecture, n'hésitez pas a poser des questions ou à ajouter des corrections sur cet article. Je ne sais pas si ce genre d'articles peut vous intéresser alors n'hésiter pas à me le faire savoir si vous en voulez d'autres.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!