Per chi è interessato a questa serie di post, consiglio prima di leggere i precedenti dato che contengono le parti fondamentali per comprendere il seguito, ecco la lista:

Parti precedenti

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-i-introduzione

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-ii

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-iii

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-iv

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-v

https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-vi

L'ultima volta mi ero fermato ad un teorema sulla condizione di esattezza di una 1-forma differenziale.

In questo post vedremo alcuni lemmi, definizioni e teoremi di base sulle serie di potenze, un prima proposizione sul raggio di convergenza.

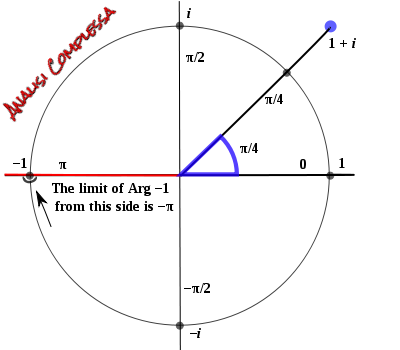
Public Domain.

Lemma.

Sia A ⊂ ℝ^2 aperto connesso, siano p,q ∈ A due punti, allora ∃ una poligonale spezzata contenuta in A che congiunge p e q.

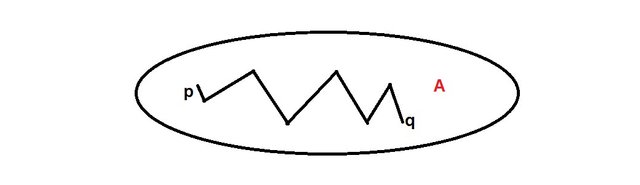
Lemma.

Siano A ⊂ ℝ^2 aperto, f ∈ C^1(A) con δf/δx = δf/δy = 0 , γ: [a,b] → A cammino di classe C^1 (dove γ(t)= ( x(t), y(t) ) ) , allora:

f(γ(a)) = f(γ(b)) ⇔ lungo il cammino f è costante, ovvero se la derivata è nulla (perché la derivata di una costante è zero).

Definizione, Serie di Potenze.

Siano 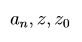∈ ℂ , una serie del tipo 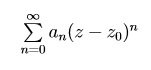è detta serie di potenze di centro z_0 e coefficienti a_n.

Si può definire quando il limite per N → ∞ coincide con la sommatoria sopra vista (con N al posto di ∞ ).

Osservazione.

Il centro z_0 della serie può essere scelto arbitrariamente, per comodità si sceglie in genere 0 come centro della serie, tutti i teoremi restano validi a prescindere dal centro che si sceglie.

Definizione, serie convergente assolutamente.

Una serie si dice convergente quando il limite delle sue somme ha un valore finito.

Una serie convergente 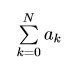si dice che converge assolutamente se converge .

Definizione, serie convergente assolutamente.

Una serie si dice che converge normalmente se 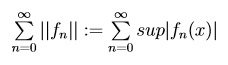converge.

Teorema.

Sia f(z) = 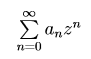, se la serie converge in z_0 ≠ 0 allora ∀ r t.c. 0 < r < |z_0| la serie converge assolutamente normalmente in r.

Proposizione e raggio di convergenza.

Sia f(z) = 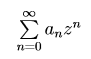, allora ∃ ρ ∈ [0,+∞[ t.c. ∀ z:

1. Se |z| < ρ ⇒ f(z) converge
2. Se |z| > ρ ⇒ f(z) non converge

ρ di questa proposizione si definisce il raggio di convergenza della serie f(z), il cui disco è {z ∈ ℂ t.c. |z| < ρ }

---

N.B. Tutti i simboli matematici riportati sono stati realizzati grazie a LaTeX Base.