Introducción a las Ecuaciones Diferenciales Parciales | Lección #2

Saludos queridos lectores, bienvenidos nuevamente. En esta oportunidad les traigo la segunda Lección de la serie Introducción a las Ecuaciones Diferenciales Parciales (EDP), en la misma desarrollaremos este tan importante e interesante tema, en donde podemos aprender muchas aplicaciones, sobre todo en el campo de la física, química, biología y otras ciencias, así como no podemos dejar de mencionar sus aplicaciones a la ingeniería y carreras afines. En la gama de problemas que se modelan con Ecuaciones Diferenciales Parciales, podemos mencionar algunos como: la propagación del calor, la propagación del sonido, la dinámica de fluidos, entre otros. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, ecuaciones diferenciales ordinarias, geometría diferencial, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Otras consideraciones acerca de Campos Vectoriales y Curvas Integrales

Como ya lo habiamos comentado en la publicación anterior (Introducción a las Ecuaciones Diferenciales Parciales | Lección #1), si queremos hallar las curvas integrales de un campo vectorial, esta la podemos considerar como las intersecciones de superficies, las cuales podemos representarlas de la siguiente manera:

si las funciones u y v satisfacen la condición siguiente:


entonces, para cada par de constantes c₁ y c₂ que tomen valores apropiados, las superficies u y v representan una curva. Geométricamente, la condición (1) significa que los gradientes de dichas funciones no son paralelos en ningún punto del dominio de ambas superficies, por lo tanto se interceptan, y por ende su intersección será una curva integral del campo vectorial asociado a ellas. El gráfico siguiente nos permite visualizar lo que hemos descrito anteriormente.


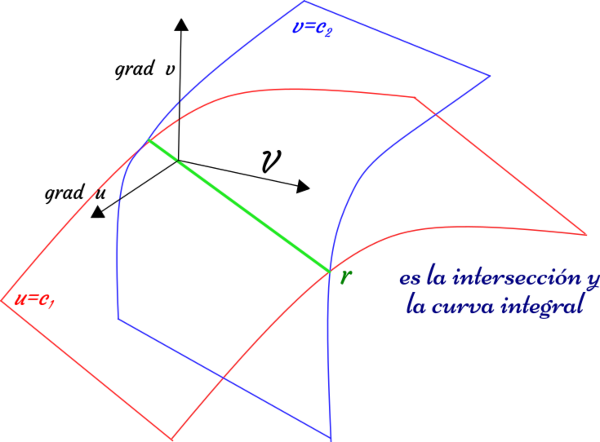
_{Imagen elaborada por @abdulmath con Inkscape.}

De esta forma podemos entonces escribir la siguiente definición:

Sean

dos superficies que son solución de


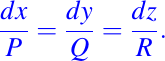
Si estas dos funciones son funcionalmente independientes entonces, para un par de valores apropiados de las constantes c₁ y c₂, las ecuaciones representan una curva integral del campo vectorial asociado sobre el dominio del mismo.

Ahora bien, si r es una curva representada por las ecuaciones anteriores. Luego, en cada punto de r,
los vectores gradientes de las superficies ya mencionadas son normales a la curva integral r. Entonces, deben satisfacer las siguientes condiciones:

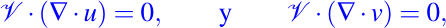
por lo tanto, tenemos:

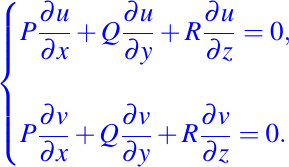
A continuación mostraremos la siguiente definición:

Notemos que la ecuación dada en (3) es una Ecuación Diferencial Parcial en la función incógnita u que depende de tres variables independientes x, y, z. Debido a la definición anterior, podemos decir que dada cualquier solución de la EDP (3), esta es una integral primera del campo vectorial asociado.

Ahora mostraremos dos teoremas que nos permite identificar cuando tenemos una integral primera de un campo vectorial dado.

Este teorema lo que nos dice que es dadas dos integrales de primera de un campo vectorial dado, podemos construir o hallar una colección de integrales de primera del campo vectorial asociado. La demostración del mismo es muy sencilla, y como dijimos al inicio de esta serie de publicaciones, obviaremos la demostración, la cual el lector interesado puede consultar en cualquier de las referencias al final de esta publicación.

El teorema que acabamos de enunciar, lo que nos dice es que si tenemos una función continuamente diferenciable por lo menos una vez, y tenemos una integral primera de un campo vectorial dado, entonces la composición de esta función con la integral primera, sigue siendo una integral primera del campo vectorial asociado, análogamente para una función de dos variables, el caso general también se satisface, es decir, que si tenemos una función de n variables continuamente diferenciable, y tenemos n integrales primera de un campo vectorial dado, la composición también es una integral primera. Al igual que en el teorema anterior, el lector interesado puede consultar la demostración en las referencias correspondientes que anexaremos al final de la publicación.

---

---

Algunos Ejemplos

A continuación mostraremos 3 ejemplos ilustrativos de lo que hemos descrito hasta el momento.

1. Consideremos el campo vectorial dado por:
   
   
   Los ceros en los denominadores no deberían de preocuparnos, pues, el hecho de que aparezca un cero en el denominador significa lo siguiente
   
   
   Como u_x=0$, lo que nos dice que una función que satisface esta ecuación es una función que no depende de la variable x, por lo tanto cualquier función que dependa de y y z únicamente es una solución de la EDP, por ejemplo:
   
   
   las cuales son dos soluciones que son trivialmente funcionalmente independientes. Ahora, las funciones
   
   
   son también integrales primeras funcionalmente independientes, y las curvas integrales del campo vectorial dado pueden ser descritas por las ecuaciones:
   
   
   para obtener la misma curva integral del campo vectorial con los dos pares de integrales primeras, debemos obviamente usar diferentes valores de las constantes c₁ y c₂
2. Sea el campo vectorial descrito por
   
   
   cuyo dominio esta determinado por el octante donde x>0, y>0, z>0. Luego, una integral primera de del campo vectorial dado es una solución de la ecuación siguiente:
   
   
   así, como ya mencionamos anteriormente el sistema asociado esta dado por
   
   
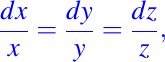
   por lo tanto si tomamos las primera igualdad, es decir
   
   
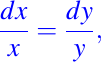
   obtenemos
   
   
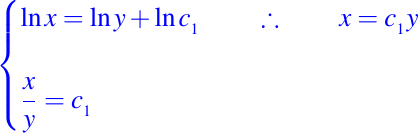
   es una integral primera del campo vectorial definido en el primer octante. Si ahora tomamos la siguiente igualdad, es decir:
   
   
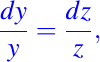
   obtenemos lo siguiente:
   
   
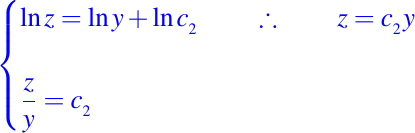
   la cual también es una integral primera del campo vectorial en el primer octante. Así que las funciones dadas por
   
   
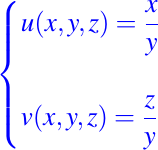
   son integrales primeras del campo vectorial sobre el primer octante. Comprobemos que son funcionalmente independientes, es decir,
   
   
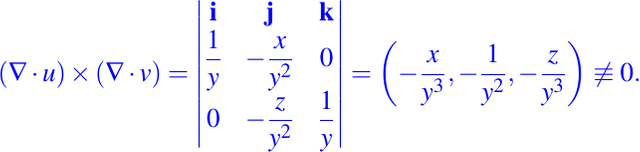
   Si damos una representación paramétrica de las curvas integrales del campo vectorial en el primer octante como sigue:
   
   
   Luego, es fácil verificar usando cálculo directo, que cualquier función de u y/ó v es también una integral primera del campo vectorial dado. Por ejemplo: Si tenemos f(u)=u², entonces,
   
   
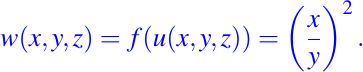
   es una integral primera del campo vectorial dado. Si ahora, tenemos f(u,v)=u²-v², entonces:
   
   
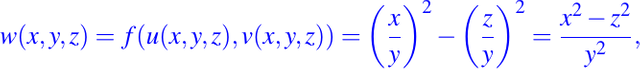
   es una integral primera del campo vectorial dado. De manera similar,
   
   
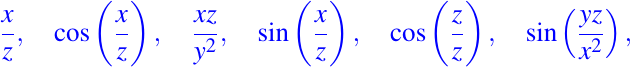
   son también todas integrales primeras del campo vectorial dado en el primero octante.
3. Consideremos el campo vectorial dado por:
   
   
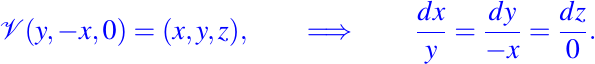
   y cuyo dominio es todo el espacio euclidiano R³ menos el eje Z. Una integral primera del campo vectorial dado es una solución de la ecuación dada por:
   
   
   como ya describimos al inicio del ejemplo, tiene como sistema asociado el siguiente:
   
   
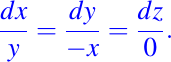
   Ahora si tomamos la primera igualdad, es decir,
   
   
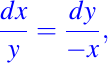
   obtenemos
   
   
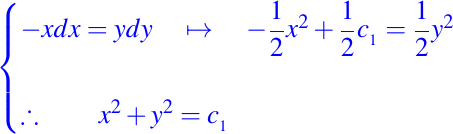
   es una integral primera del campo vectorial sobre el dominio dado. Si ahora tomamos la segunda igualdad, es decir,
   
   
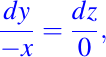
   obtenemos
   
   
   la cual también es una integral primera del campo vectorial dado sobre el dominio. Así, las integrales primeras del campo vectorial dado, son:
   
   
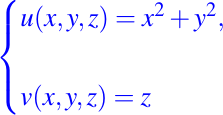
   Comprobemos que estas funciones son funcionalmente independientes, para ello se debe verificar lo siguiente:
   
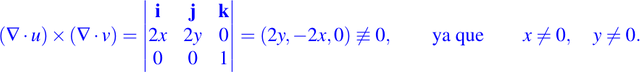
   Por lo tanto u y v son funcionalmente independientes. Las curvas integrales descritas por
   
   
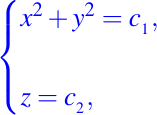
   forman círculos concéntricos paralelos al plano XY y centradas en el eje Z. Similarmente, tenemos otras superficiens dadas por:
   
   
   las cuales también son integrales primeras del campo vectorial dado.

---

---

Queridos amigos y lectores, espero hayan disfrutado y aprendido en esta segunda Lección de la serie de Introducción a las Ecuaciones Diferenciales Parciales, de igual manera los invito para la tercera Lección de esta serie, donde continuaremos tratando este tema tan interesante y de mucha aplicación. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Lang, Serge. Calculus of Several Variables. Springer Science & Business Media, 2012.
• Edwards, Charles Henry. Advanced Calculus of Several Variables. Courier Corporation, 2012.
• Dennemeyer, Rene. Introduction to Partial Differential Equations and Boundary Value Problems. 1968.
• Pinchover, Yehuda, and Jacob Rubinstein. An Introduction to Partial Differential Equations. Cambridge University Press, 2005.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales Parciales, que estoy seguro serán de su interés:

Introducción a las Ecuaciones Diferenciales Parciales - Lección #1

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por abdulmath usando software libre, , GIMP e Inskcape.

---

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}