Modelos Continuos de Población | El modelo Crecimiento exponencial y El Modelo Logístico de Población

Por ejemplo, la propagación de una enfermedad en una gran población a través de la introducción de un solo individuo infectado conduce a la generación de casos secundarios. El medio ambiente está libre de competencia intraespecífica, al menos al comienzo del brote, cuando una gran población de susceptibles proporciona un suministro prácticamente ilimitado de hospedantes. En resumen, la propagación de la enfermedad en una gran población de susceptibles puede considerarse como un proceso de invasión a través de contactos independientes con unos pocos individuos infectados.
Esta publicación esta dirigida a estudiantes, profesionales e investigadores en especifico en el área de las ciencias Biológicas, o Matemáticas, y al publico interesado en estos temas interesantes para el entendimiento de parte del medio que nos envuelve en el día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.


La tasa de cambio del tamaño de la población puede calcularse si se conocen las tasas de natalidad, mortalidad y de migración. Una población cerrada es aquella que no tiene migración hacia o desde la población, es decir, el tamaño de la población cambia solo a través de los nacimientos y las muertes, así la tasa de cambio del tamaño de la población es sencillamente la tasa de natalidad menos la tasa de mortalidad.
La formulación de un modelo específico requiere de suposiciones explícitas sobre las tasas de natalidad y mortalidad. Idealmente, estas suposiciones se hacen con el objetivo de abordar cuestiones biológicas específicas como, por ejemplo, ¿en qué condiciones la competencia entre especies conducirá a la coexistencia?
Para los microorganismos, que se reproducen por división, es razonable suponer que la tasa de nacimiento de nuevos organismos es proporcional al número de organismos presentes. En términos matemáticos esta suposición puede expresarse diciendo que si el tamaño de la población en el tiempo t es x entonces, en un intervalo de tiempo corto de duración, digamos de magnitud h, es decir, un intervalo de tiempo [t, t+h], el número de nacimientos es aproximadamente igual bhx, donde b es una constante, de la tasa de natalidad per cápita.
De manera similar, podemos asumir que el número de muertes en el mismo intervalo de tiempo es aproximadamente igual a μhx, donde μ es una constante, de la tasa de mortalidad per cápita.
Por lo tanto, el cambio neto en el tamaño de la población en el intervalo de tiempo [t, t+h], es x(t + h) - x(t), el cual puede ser aproximado por [bh - μh)]x(t). La magnitud del intervalo de tiempo debe ser corta para garantizar que el tamaño de la población no cambie mucho y que, por lo tanto, el número de nacimientos y defunciones sea aproximadamente proporcional a x(t). En otras palabras, tenemos la siguiente ecuación aproximada

Si dividimos por h obtenemos

fácilmente podemos identificar del lado izquierda de la aproximación anterior la tasa de cambio de la población con respecto al tiempo, es decir, que formalmente si tomamos el límite cuando h tiende a cero, obtenemos la siguiente ecuación

todo esto, suponiendo que la la función x(t) es diferenciable.
La aproximación dada en (1) lo que significa es que la diferencia entre los valores de los dos lados de la aproximación es tan pequeña que el resultado de dividir esta diferencia entre h es una cantidad tan pequeña que se aproxima a cero cuando la magnitud del intervalo es cero, es decir, cuando el valor de h tiende a cero (como lo dijimos anteriormente, estamos suponiendo que los intervalos de tiempo donde se estudia el cambio son pequeños).
Si la tasa de crecimiento neto la definimos de manera natural como

así tenemos otra forma de ver el mismo modelo, observando que si el tamaño de la población en el instante de tiempo t es x(t), entonces en el siguiente intervalo de tiempo (pequeño) de longitud h, el incremento neto en el tamaño de la población producido por un solo organismo será rh.
Ahora bien, debido a que todos los individuos son independientes (sin competencia en un entorno sin restricciones) entonces el incremento neto en la población producto de todos los organismos x(t) será rhx(t) y por lo tanto llegamos de nuevo a la ecuación diferencial siguiente

Esta ecuación diferencial tiene una familia infinita de soluciones dada por la familia de funciones de un parámetro

por lo tanto, esta familia de parámetros da una solución a la ecuación mostrada en (4) para cada elección de la constante k. La forma más conveniente de imponer una condición que describa la dinámica poblacional de una población específica es especificando el tamaño inicial de la población, es decir, en el momento de tiempo t = 0, de la siguiente manera

con esta condición dada anteriormente esta opción selecciona la solución

La condición dada en la ecuación (5) se denomina condición inicial y el problema que consiste en la ecuación diferencial dada en (4) junto con la condición inicial (5) se denomina problema de valor inicial.
Como se ha señalado anteriormente, el problema del valor inicial anterior tiene la solución única, ahora bien si r > 0 (o su equivalente b > μ) implica que el tamaño de la población crece sin límites cuando el tiempo t tienda a infinito, mientras que si r < 0 (o su equivalente b < μ) implica que el tamaño de la población se acercará a cero cuando t tiende a infinito.
En ausencia de nacimientos, es decir, b = 0, la población se ve deplorada por muertes a razón de la tasa μ y, en consecuencia, la esperanza de vida media de un miembro de esta población es de 1/μ.
Si b > 0 entonces el número promedio de descendencia durante la vida de un individuo promedio, bajo el modelo de Malthus sería b/μ. Si esta proporción, la cual generalmente se denominada número o razón reproductiva básica R0, es superior a uno, entonces los nacimientos superan a las muertes y el número medio de hijos por persona a lo largo de su vida es superior a uno, es decir, la población explota; si esta proporción es inferior a uno, entonces las muertes superan a los nacimientos, el número medio de hijos por persona es inferior a uno, y la población se extingue.
La predicción de que el tamaño de la población crecerá exponencialmente bajo estas condiciones, como ya lo hemos dicho anteriormente (ver La Biología y las Matemáticas) fue formulado por primera vez por Malthus (1798). Malthus predijo el desastre ya que no era posible aumentar el suministro de alimentos para mantener el ritmo de crecimiento de la población a una tasa de crecimiento per cápita positiva constante. Las poblaciones que crecen exponencialmente al principio son comúnmente observadas en la naturaleza. Sin embargo, sus tasas de crecimiento suelen tender a disminuir a medida que aumenta el tamaño de la población. De hecho, el crecimiento exponencial o la decadencia pueden considerarse un comportamiento local típico.
En otras palabras, la dinámica de las poblaciones puede ser aproximada por este modelo simple solo por períodos cortos de tiempo; es decir, la dinámica de una población puede ser bien manejada localmente con modelos lineales. La suposición de que la tasa de crecimiento de una población es proporcional a su tamaño suele ser poco realista en escalas de tiempo más largas. A continuación examinaremos los supuestos no lineales sobre la tasa de crecimiento de la población, que dan lugar a predicciones cualitativas muy diferentes.



El estudio de los modelos en los que la tasa de crecimiento depende solo del tamaño de la población, a pesar de sus deficiencias, estos modelos permiten predecir el comportamiento cualitativo de muchas poblaciones reales. La tasa de crecimiento per cápita, o tasa de crecimiento por miembro, viene dada por
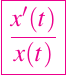
el cual estamos asumiendo es una función de x(t). Anteriormente, asumimos que la la tasa de crecimiento total es proporcional al tamaño de la población (un modelo lineal) o, equivalente, tomamos una tasa de crecimiento per cápita constante. Ahora, se consideran las tasas de crecimiento que disminuyen a medida que aumenta el tamaño de la población.
El modelo de población más simple en el que la tasa de crecimiento per cápita es una función decreciente del tamaño de la población es λ-ax. Esta suposición conduce a la ecuación diferencial logística
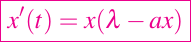
el cual fue introducido por primera vez por Verhulst (1838) (ver La Biología y las Matemáticas) y posteriormente estudiado por R. Pearl y L. J. Reed (1920). Esta ecuación se escribe comúnmente de la siguiente forma

con los parámetros r = λ, K = λ/a. A estos parámetros r y K, que se suponen positivos, se les puede dar entonces un significado biológico. Observemos que x' es aproximadamente igual a rx cuando el valor de x es pequeño, y que x' = 0 cuando x está cerca de K. En otras palabras, cuando x es pequeño la población experimenta un crecimiento exponencial, mientras que cuando x está cerca de K la población apenas cambia.
Ahora bien, necesitamos un método para resolver la ecuación dada en (6), entonces tenemos el método de separación de variables, para resolver ecuaciones diferenciales de este tipo (ver Introducción a las Ecuaciones Diferenciales Ordinarias | Lección #2), el cual nos permite reescribir la ecuación (6) de la siguiente forma
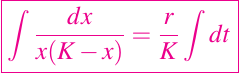
ahora para resolver la integral de la izquierda, debemos usar el método muy conocido llamado método de fracciones parciales, obteniendo así como resultado
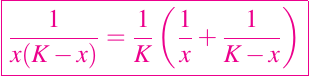
luego sustituyendo en la integral anterior e integrando, obtenemos
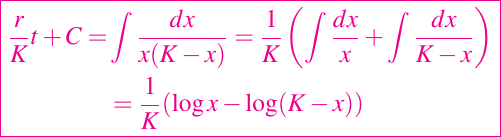
donde C es la constante de integración.
Si el tamaño de la población en el momento t = 0 es x0, entonces la condición inicial es x(0) = x0, y luego de sustituir en la solución dada arriba, obtenemos el valor de la constante C el cual está dado por
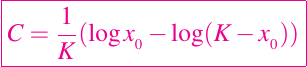
Sustituyendo en la solución el valor de la constante C y realizando algunas simplificaciones algebraicas (las cuales omitiré para no abrumarlos con tanta matemática) obtenemos la solución general dada de la siguiente manera
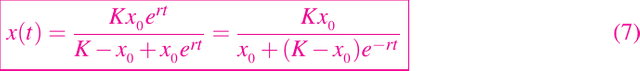
De esta manera podemos decir, que la solución obtenido solo es válida si 0 < x0 < K, para garantizar que los logaritmos obtenidos en la integración estén definidos. Para obtener la solución sin esta restricción, nuestra integración debería haber dado logaritmos en valores absolutos. Sin embargo, la fórmula dada en (7) para la solución de la ecuación logística es válida para todos los x0, como podría verificarse mediante un análisis más cuidadoso.
La expresión dada por (7) para la solución del problema del valor inicial logístico muestra que el tamaño de la población x(t) se aproxima al límite K cuando el tiempo t tiende a infinito, si x0 >0. El valor K se llama la capacidad de carga de la población porque representa el tamaño de la población que los recursos disponibles pueden seguir apoyando. El valor r se denomina tasa de crecimiento intrínseco porque representa la tasa de crecimiento per cápita alcanzada si el tamaño de la población fuera lo suficientemente pequeño como para asegurar limitaciones insignificantes de recursos. El modelo logístico predice un rápido crecimiento inicial de 0 < x0 < K, y luego una disminución en la tasa de crecimiento a medida que pasa el tiempo, de modo que el tamaño de la población se acerca a un límite. Este comportamiento está de acuerdo con el comportamiento observado de muchas poblaciones, y por esta razón, el modelo logístico se utiliza a menudo como medio para describir el tamaño de la población.



Con estas suposiciones, podemos escribir el siguiente modelo:
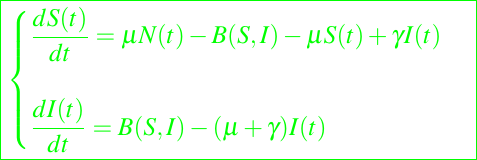
donde B(S, I) denota la tasa de incidencia, es decir, el número de nuevos casos de infección por unidad de tiempo. Obviamente, B(S, 0) = B(0, I) = B(0, 0) = 0, es decir, si no hay susceptibles o infectados o ambos, entonces no debería haber nuevos casos de infección. Por lo tanto, es plausible suponer

Si suponemos que C denote el número promedio de parejas sexuales por individuo por unidad de tiempo y a φ que denota el número promedio de contactos por pareja, entonces φCS(t) denota el número total de contactos por unidad de tiempo de todos los individuos susceptibles en el momento. Si todos los individuos se mezclan al azar entonces el número de contactos sexuales por unidad de tiempo entre los susceptibles sería
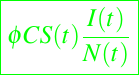
y en consecuencia tenemos

Además, si asumimos que solo una fracción q (con q tomando valores entre 0 y 1, inlcusive) de estos contactos se convierten en nuevos casos de infección. Definiendo la tasa de transmisión como β = qφC, llegamos a la siguiente expresión para la tasa de incidencia en una población que se mezcla aleatoriamente:
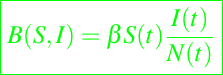
De esta manera el modelo se convierte en el siguiente:
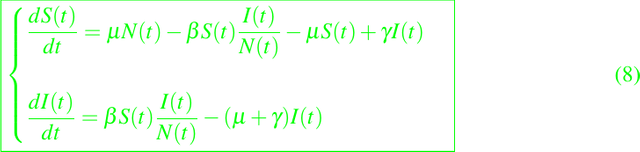
con N = S + I, y condiciones iniciales S(0) = S0 > 0, I(0) = I0 > 0. Ya que
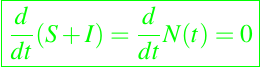
la tasa de natalidad es igual a la tasa de mortalidad y el tamaño total de la población es constante. La sustitución

donde N es una constante, reduce la solución del sistema dado en (8) a la solución de la ecuación diferencial simple
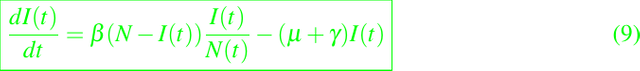
ó
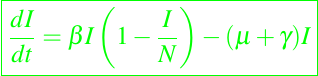
ó
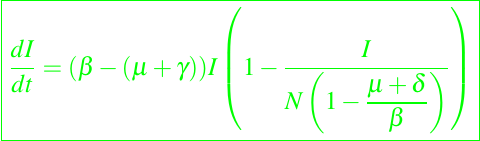
ó
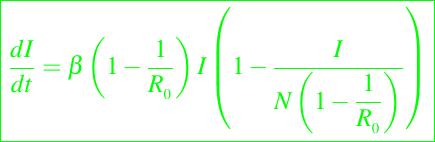
donde
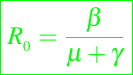
Si definimos ahora a r y K como sigue
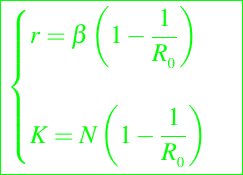
obtenemos la forma de la ecuación logística
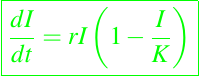
Por lo tanto, si R0 > 1 entonces r > 0, K > 0, e I ---> K. Si R0 < 1 entonces r < 0, K < 0, e I ---> 0.
Por supuesto, K < 0 no tiene sentido biológico. Por lo tanto, concluimos que existe un equilibrio positivo (endémico) I∞ > 0 existe y es abordado por soluciones si y sólo si R0 > 1; de lo contrario, el único equilibrio biológico es I∞ = 0, que se aborda mediante soluciones si R0 es menor o igual a 1, pero no si R0 > 1.
Queridos amigos y lectores, espero hayan disfrutar de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en las ciencias sociales, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Anónimo, An Essay on the Principle of Population, as it affects the future improvement of society with remarks on the speculations of Mr. Godwin, 1798.
- Cohen, J. E. How Many People Can the Earth Support? W. W. Norton and Company, New York-London, 1995.
- Eugene M. Izhikevich. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Massachusetts Institute of Technology, 2007.
- Fred Brauer, Carlos Castillo-Chávez, Elmer De La Pava-Salgado, Kamal Barley, Carlos W. Castillo-Garsow, Diego Chowell, Baltazar Espinoza, Paula González Parra, Carlos Hernández Suárez, Víctor M. Moreno. Modelos de la propagación de enfermedades infecciosas. Universidad Autónoma de Occidente. Cali, Colombia. 2015
La imagen de fondo de la portada es una imagen de libre uso tomada de y editada con GIMP por @abdulmath. Las imágenes son todas de libre uso, tomadas de
y editadas y tratadas con GIMP. Los títulos, imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, LaTeX2e, Inkscape y GIMP.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Agradecido por la nominación y el apoyo.
Saludos cordiales.
Excelente trabajo el que nos presentas sobre Dinámica Poblacional, amigo @abdulmath. Gracias por compartirla. Saludos.
Muy agradecido por su visita, comentario acerca de este trabajo. Un gran esfuerzo, en lograrlo. Gracias amigo @tsoldovieri.
Saludos Cordiales.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Hi @abdulmath!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations @abdulmath! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
Interesante tu artículo @abdulmath. Es posible que esté en la misma onda de investigación de esta belleza de Cambridge.
Hola @dougjim, agradecido por tu comentario, que se que viene de muy buena fuente. Interesante el artículo, además de ser una mujer muy linda (cosa rara en nuestro circulo matemático).
Saludos y éxitos, un fuerte abrazo.
Pocas personas son capaces de dar temas de matemáticas de forma tal que las personas puedan entenderla, de verdad te felicito amigo, con tu post repase un poquito de este tema, muy importante en mi carrera.
Hola @andreacastaneda, que bueno verte de nuevo por mi blog, y gracias por tus comentarios. Espero que haya sido de tu agrado, y verte otra vez visitando mi blog.
Saludos y un fuerte abrazo.
Interesante tema, poder apreciar las matemáticas desde otra perspectiva me permite comprobar que ella es la reina de las ciencias. Actualmente me encuentro trabajando con mi tesis y dentro de las teorías que estoy tratando se encuentra la teoría de sistemas y la teoría de juegos todo para el estudio de la gerencia, entonces las matemáticas están inmersas en todo ese transitar investigativo. Me agradó leerte y te felicito nuevamente por tu trabajo constante y de calidad.
Buena vibra.
Hola @angelica7, aunque suene quizás pedante decirlo, pero las matemáticas son las reinas de todas las ciencias, y todo nuestro mundo y el universo gira alrededor de las matemáticas, ellas están presentes en cada cosa que hacemos a diario, aunque por sencillo sea. Que bueno saber que stas estudiando y aplicando la teoría de juegos, es un tema súper apasionante, la última vez que lei algo acerca de eso, fue parte de la tesis doctoral de John Nash (premio Nobel de Economía). Felicitaciones y éxitos en tu trabajo.
Saludos cordiales, y te envió un fuerte abrazo.
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Excelente artículo, muy relacionado con mi área temática.. me deleito con cada palabra! cada vez mejor Doctor

Hola @alexaivytorres, me contenta saber que disfruta de mis escritos. Agradecido por tu tiempo en leerlo y disfurtarlo.
Saludos Cordiales.