En primer lugar mis saludos respetuosos para toda la comunidad de #stem-espanol, #steemstem, #utopian-io y #proconocimiento, así como para el resto de la prestigiosa comunidad de steemit, continuando con la temática geometría analítica plana, en donde hemos ido dando importantes pasos hacia el desarrollo analítico de las matemáticas y con ello la debida comprensión de numerosas áreas tanto académicas como profesional, a través de la geometría analítica plana ya que esta parte de las matemáticas (geometría analítica plana) representa el principio fundamentar para tales propósitos, les dejo el enlace de la pasada publicación.

Geometría analítica plana I parte.

En esta oportunidad seguiremos profundizando en esta temática con puntos tales como:

Distancia entre dos puntos ahora en el plano:

El estudio de los puntos tanto en un sistema lineal o unidimensional como en el plano o el espacio, representa para la geometría analítica el epicentro del entendimiento y conformación de cualquier figura geométrica, ya conocimos la distancia entre dos puntos en un sistema lineal, la cual representa la longitud numérica de un determinado segmento dirigido, ahora estudiaremos o analizaremos la distancia entre dos puntos en el plano, con la finalidad de poder realizar una serie de estudios tales como la demostración en cuanto a la conformación de ciertas figuras geométricas, por ejemplo, poder conocer un determinado tipo triángulo por medio de la distancias que están determinadas por tres pares de coordenadas (x,y) que representan sus vértices y los cuales dan origen a la figura geométrica conocida como triángulo, para este caso será en el plano, siempre es importante recordar conocimientos anteriormente adquiridos ya que hemos partido del principio relacionado y orientado de lo más simple llegamos a la conformación de lo más complejo, entonces podemos decir, que en el sistema lineal un determinado punto está restringido sobre la recta o eje dirigido (orientado), en cambio en el plano podemos tener mayor movilidad de un determinado punto el cual estará asociado con un único par ordenado (x,y) de números, esto siempre y cuando permanezca en el mismo plano.

Analicemos inicialmente la conformación de la fórmula de la distancia (d) entre dos puntos en el plano, es decir, P1(x1, y1) y P2(x2, y2) cuya fórmula es:

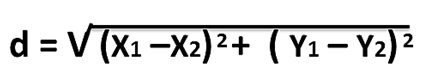
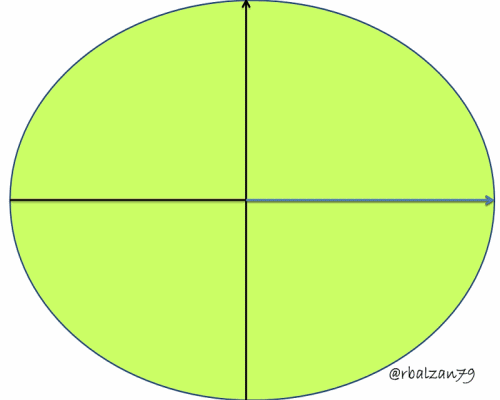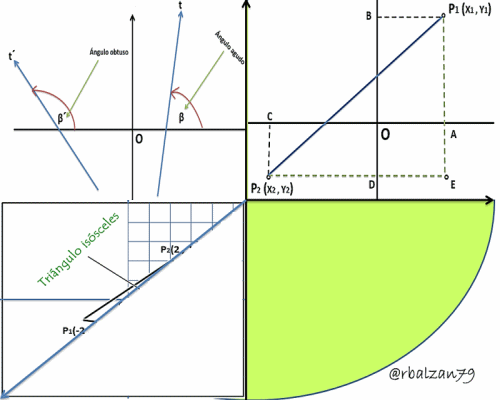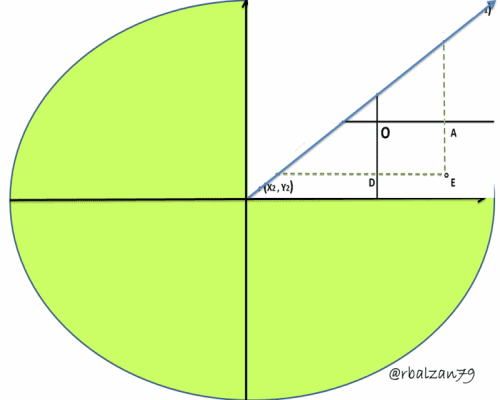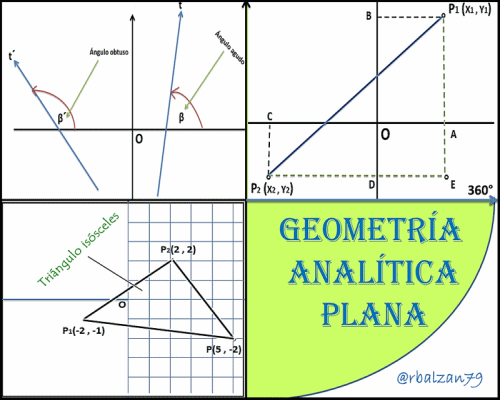
Si tenemos dos puntos cualesquiera, es decir, P1(x1, y1) y P2(x2, y2) en términos generales y queremos determinar la distancia entre ellos:

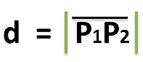
Podemos inicialmente trazar dos perpendiculares entre sí, la primera (P1A1) paralela al eje de las Y o perpendicular al eje de las X y la otra (P2B2) paralela al eje de las X o perpendicular al eje de las Y, en donde su punto de intersección lo denominaremos C, para poder apreciar mejor dicha descripción utilizaremos la siguiente figura 1 (Gif animado):

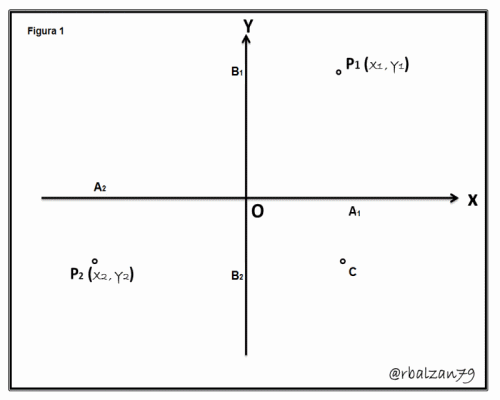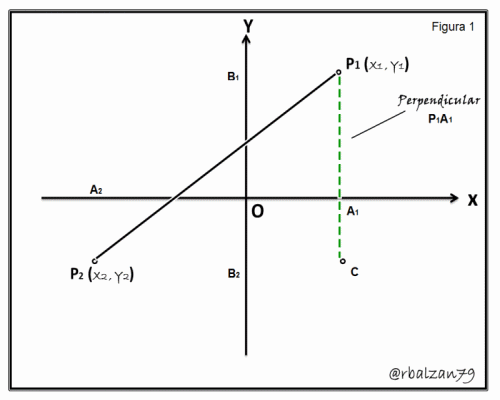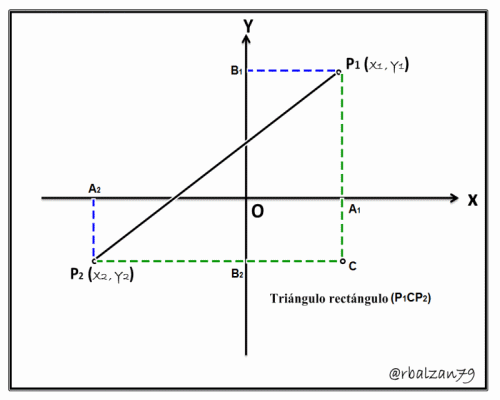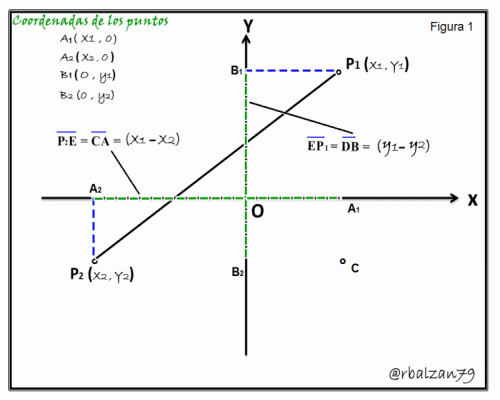
En dicha figura podemos considerar claramente para nuestro análisis el triángulo rectángulo conformado por los puntos P1CP2, y sabemos por trigonometría que mediante el teorema de Pitágoras, tenemos:

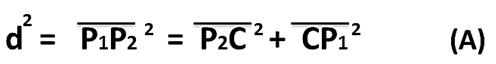
Por lo tanto, las coordenadas de cada uno de los puntos que intervienen en las bases de dichas perpendiculares a los ejes coordenados son:

A1(x1, 0) ; A2(0 , y1) ; B1(x2 , 0) ; B2(0 , y2), con estas coordenadas podemos decir que:

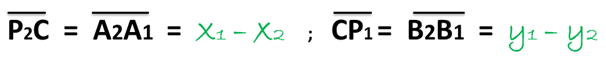
Ahora con estos valores podemos determinar la fórmula de la distancia entre dos puntos en el plano al sustituir los mismos en el planteamiento inicial (A) del teorema de Pitágoras:

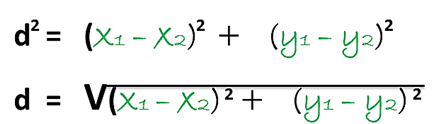
De esta manera hemos obtenido la fórmula de la distancia entre dos puntos dados cuyas coordenadas correspondan a un determinado plano cartesiano.

Al observar la anterior demostración de la fórmula, podemos seguir haciendo hincapié en la adecuada construcción del conocimiento, es decir, partiendo de lo básico elemental a lo amplio y complejo, constantemente como docentes es necesario tener presente la siguiente interrogante:

¿Será siempre importante entrelazar conocimientos previos con conocimientos recientemente adquiridos para la obtención de nuevos aprendizajes?

Con la conformación de esta fórmula (distancia entre dos punto en el plano) podemos dar un ejemplo concreto con respecto a la utilización de conocimientos previos y recientemente obtenidos para poder adquirir nuevos aprendizajes; observemos que gracias a todas las características analíticas inyectadas a un segmento dirigido nos ha servido como base fundamental primeramente para la estructuración de sistemas coordenados lineales o bidimensionales, y estos sistemas a su vez lo utilizamos tanto para el estudio analítico de figuras geométricas, así como en la conformación y demostración de algún tipo de formulaciones, apoyándonos además en el lenguaje universal del álgebra, es decir, mediante la utilización de letras, números y símbolos, logrando así un aspecto de generalidad como ya hemos expresados pero que siempre es importante resaltar.

Para este análisis por ejemplo, podemos resaltar la implementación de la trigonometría y el álgebra (conocimientos previos) mediante la aplicación concreta del teorema de Pitágoras a un triángulo rectángulo (P1CP2) como observamos en la figura (1), sin embargo, unido a la trigonometría y el lenguaje algebraico se encuentra todo el recorrido que hemos realizado mediante la obtención de nuevos conocimientos en donde la línea trazada como una de las perpendiculares P1A1, ayudo a dar origen al triangulo rectángulo (P1CP2) al proyectarla hacia uno de los ejes en este caso (Y) mediante los puntos (B1B2) nos permitió conocer las coordenadas de dicha perpendicular, ya que anteriormente le dimos a cada uno de estos ejes carácter de proporcionalidad en el trayecto de su longitud entre un determinado punto geométrico y un número, y que a todo punto le corresponderá un par ordenado (x,y) , es por ello que el segmento CP1 = B2B1, de la misma forma se llevó a cabo para el análisis de las coordenadas de los puntos A1, A2 y B2, y también con la relación en donde el segmento P2C = A2A1, y luego estos datos obtenidos lo introducimos en el planteamiento algebraico del teorema de Pitágoras para un triángulo rectángulo, y de esta manera adquirimos el conocimiento de la estructuración de la fórmula algebraica de la distancia entre dos puntos en el plano.

Con la fórmula de la distancia entre dos puntos en el plano, y ya constituida la utilizaremos como herramienta para la comprobación de la estructura de ciertas figuras geométricas tales como:

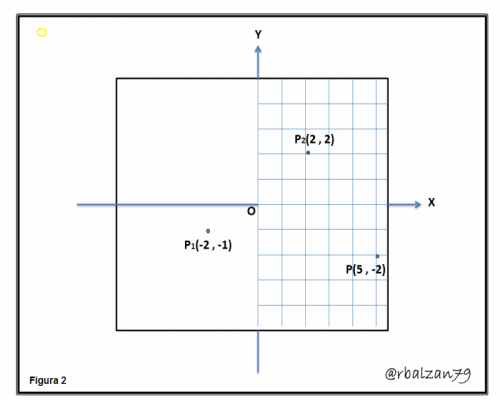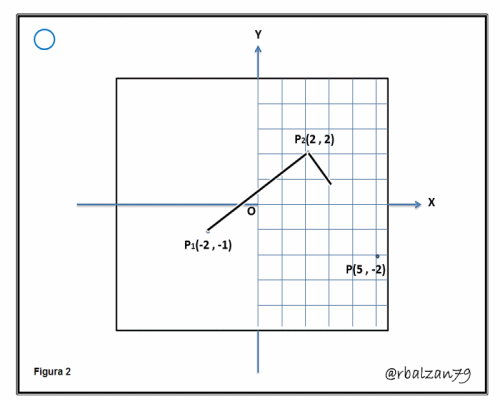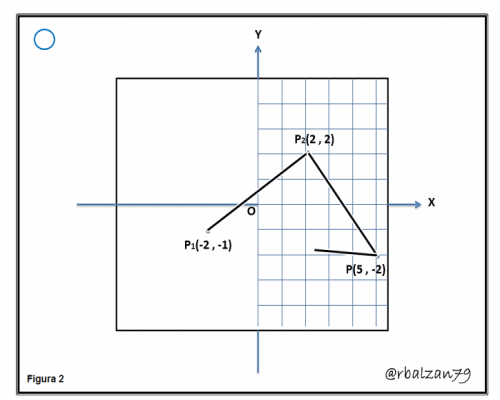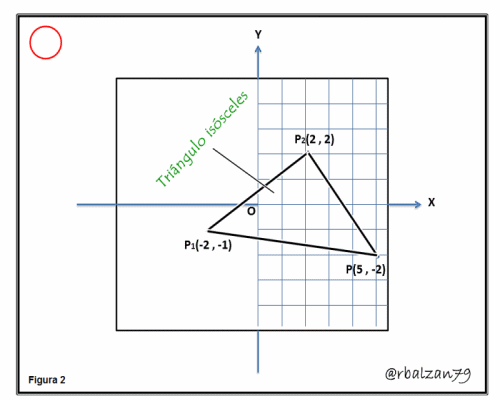
• Comprobar que los siguientes puntos cuyas coordenadas son P1(-2 , -1) ; P2(2 , 2) y P3(5 , -2), representan los vértices de un triángulo isósceles:

Entonces tenemos la siguiente fórmula de distancia entre dos puntos:

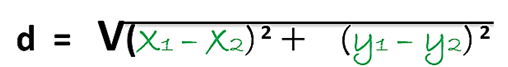
Procedemos a sustituir los valores en dicha ecuación para encontrar la longitud entre los tres puntos los cuales representan los posibles vértices de un triángulo isósceles:

Tenemos que un triángulo isósceles posee dos lados iguales; donde el tecer lado representa la base de dicho triángulo, esta condición de dos lados iguales hace que los ángulos en la base de dicho triángulo sean iguales, es decir, que analogamente podemos expresar que si dos ángulos de un determinado triángulos son iguales, tenemos que los lados opuestos de dicho triángulo serán iguales, en nuestro caso calculamos mediante la fórmula de distancia la longitud entre tres vértices de un posible triángulo isósceles, y notamos que existe una condición necesaria y suficiente para determinar que tales vértices son de un triágulo isósceles ya que dos de sus lados son iguales a cinco (5) unidades de longitud, como podemos verificar tanto en la aplicación de la fórmula de distancia entre dos puntos y en la siguiente figura animada gif.

Ángulos entre dos segmentos dirigidos:

El ángulo representa uno de los fundamentos conceptuales y prácticos de la geometría más utilizados en innumerables ramas de la sabiduría humana, pienso que quizás es una de las más poderosas y útiles de las herramientas que las matemáticas nos hayan brindado en pro de nuestro bienestar social e intelectual.

De allí es donde radica la importancia de su estudio en esta publicación, con la finalidad de conocer en términos generales sobre los mismos (ángulos) debido a que esta herramienta nos permitirá una mejor comprensión a futuro para la obtención de nuevos saberes o aprendizajes tantos matemáticos como en innumerables áreas, las cuales han encontrado en los ángulos el aliado adecuado y perfecto para la profundización y aplicación de nuevos aprendizajes, con el fin de ofrecer a la humanidad mejores beneficios sociales.

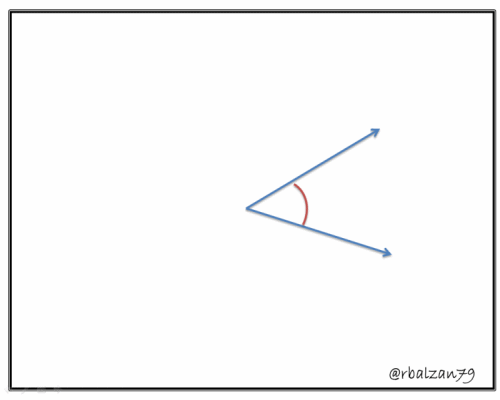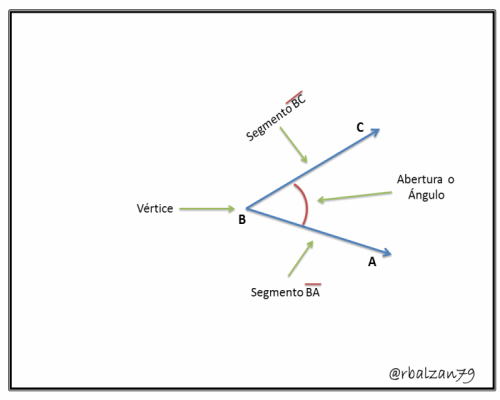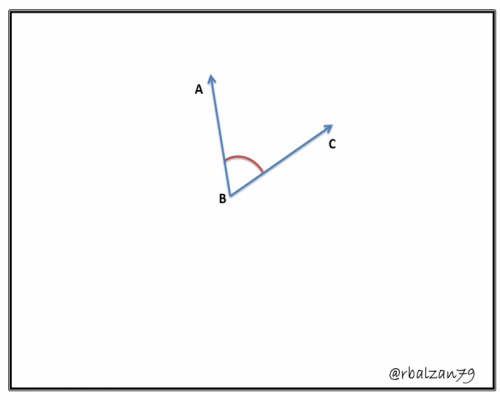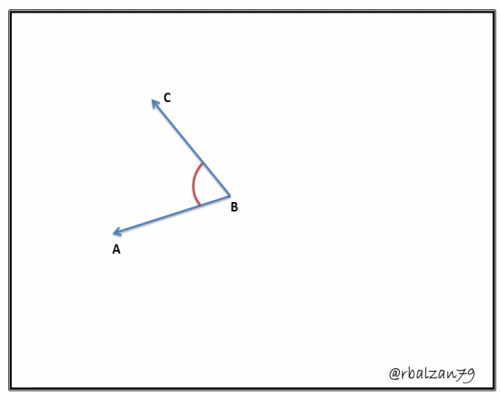
Entonces, podemos iniciar diciendo que la geometría analítica plana o espacial ha logrado profundizar el conocimiento en cualquier aspecto de las matemáticas y como hemos afirmados anteriormente impactando así en muchísimas áreas más, el estudio de los ángulos no ha escapado del valioso impacto positivo de esta importante rama, por lo tanto, decimos que un ángulo no es más que una determinada abertura que forman dos segmentos dirigidos cuyos sentidos divergen, pero que a la vez convergen en un extremo el cual lo denominamos vértice, o también podemos decir, que un ángulo es una determinada porción de un plano donde el mismo está marcado por dos segmentos dirigidos partiendo de un punto en común (vértices), claramente observamos varias expresiones creadas y donadas por la habilidad de la geometría analítica plana en la definición antes descrita, profundizando la conceptualización de la geometría elemental.

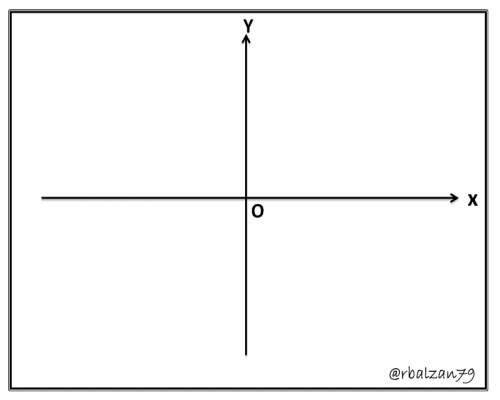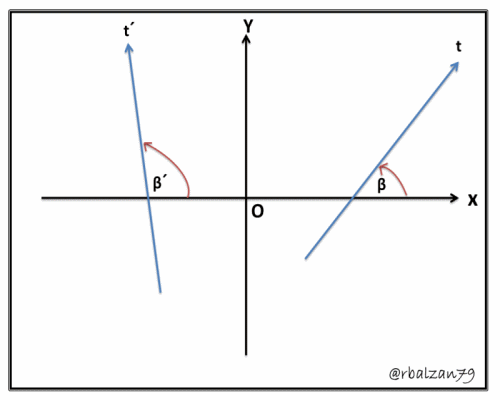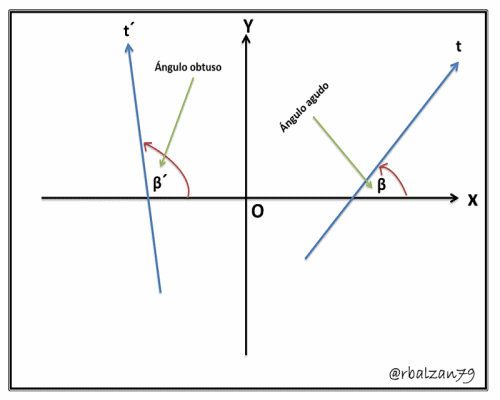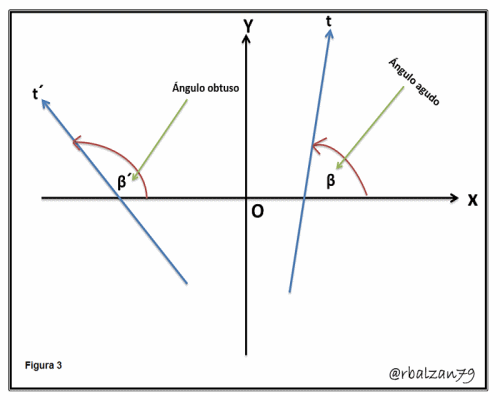
Por lo tanto, el ángulo de inclinación de una determinada recta es aquel formado por la parte o cuadrante positivo del eje de las X y dicha recta la cual es considerada con movimiento hacia arriba, ejemplo observemos la figura 3 (Gif animado):

El tratamiento de los ángulos como magnitudes encierra aspectos de complejidad, ya que es necesario contar con una serie de propiedades o un sistema de medición para tales aberturas (ángulos) que nos permita una adecuada y continua proporcionalidad mediante la descripción o trayectoria del estudio de estas aberturas, para que su aplicación sea realizada de manera eficaz, para interpretar la medición de un ángulo podemos hacerlo de varias forma, una de las medidas utilizadas son los grados centesimales, la misma consiste en dividir una circunferencia en cuatrocientas (400) partes iguales cada una representa un grado, distribuidas en cuatros cuadrantes de cien (100) partes o grados), también tenemos la medida en grados sexagesimales, para esta medida dividimos la longitud de una circunferencia en 360 partes iguales, distribuidas estas partes en cuatros cuadrantes cada uno de 90 partes o grados, esta medida de proporcionalidad es la más común o la más utilizada tanto en nuestras academias como en cualquier área profesional, por lo tanto, es la que utilizaremos para nuestro análisis de los ángulos.

Encontramos también otro tipo de proporcionalidad de medida para la longitud de una determinada circunferencia, y es la que está vinculada con los radianes (π), la cual está relacionada con la longitud del radio de la circunferencia a estudiar, esta medida de su radio es la que trazamos en cualquier arco de la circunferencia, luego de trazar la medida de dicho radio ese extremo lo unimos con el centro de tal circunferencia esto es lo que conocemos como el ángulo o abertura de un radian, por lo tanto, al compararlo con la medida sexagesimal (360°) la cual como hemos expresado es la más conocidas por todos tendríamos una relación de π = 180° o 2π = 360°, de esta manera lo podríamos relacionar para cualquier cantidad de grados sexagesimales o centesimales si así lo deseamos.

Para los estudiantes el estudio del ángulo representa uno de los conceptos más temidos debido a sus distintas formas o sistemas de medición (antes mencionados) que se utilizan para estas aberturas entre dos segmentos dirigidos, por mencionar un aspecto podemos señalar, para la medición de un ángulo es necesario relacionarlos a un arco de una circunferencia y esto es fácil observarlo cuando describimos la trayectoria de una determinada abertura o ángulo, sin embargo, en ocasiones es necesario utilizar para el cálculo de la longitud de una circunferencia una magnitud irracional, el reconocido número π, esto sin dudas, agrega complejidad o temor a nuestros estudiante al momento de una división de un ángulo cualquiera en tres o más partes iguales, por colocar solo un pequeño ejemplo, pero es importante poder detectar el método más fácil de comprender por nuestros estudiantes para brindarles confianza y luego abordar métodos más complejos (como describimos al llevar grados sexagesimales a radianes), pero siempre atentos a sus debilidades, esto nos permitirá una mejor comprensión en cualquier aprendizaje por partes de nuestros estudiantes.

Clasificación de los ángulos:

Ahora podemos conocer los tipos de ángulos más comunes o más utilizados en las distintas áreas de nuestro aprendizaje o en el ámbito profesional, recordando que utilizaremos el sistema sexagesimal por considerarlo el más conocido:

1.- El ángulo nulo, es aquel cuya abertura es de 0°, es decir, ninguna.

2.- Ángulo Convexo (0°< α <180°) para este tipo de ángulos encontramos las siguientes clasificaciones:

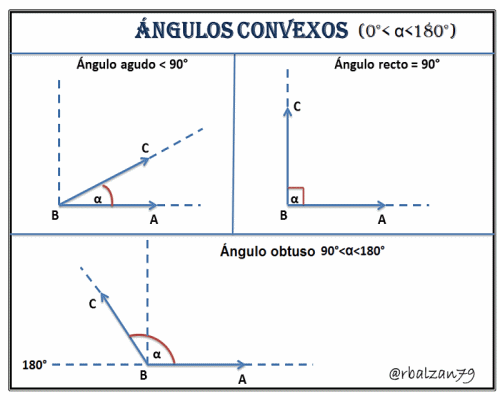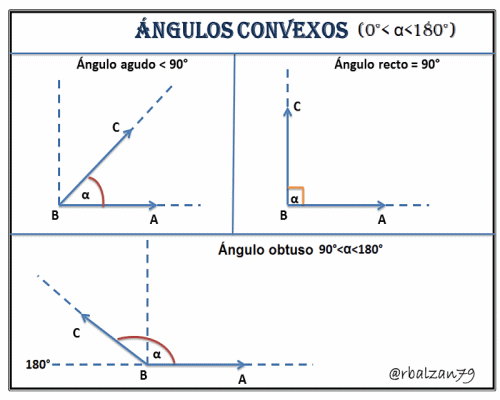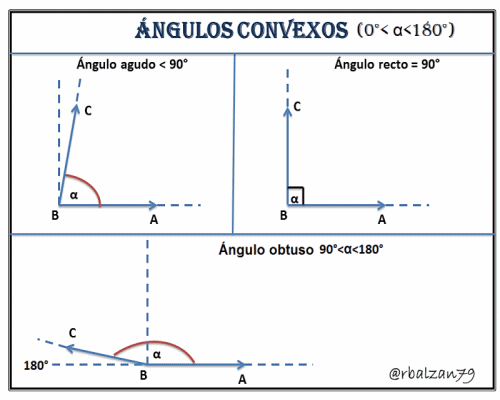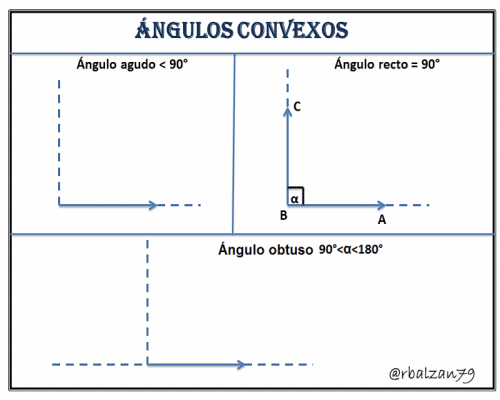
a.-) Ángulo Agudo, es un tipo de abertura que se encuentra entre los 0° y 90° pero sin tomar lates valores, es decir, 0° < α < 90°.

b.-) Ángulo Recto, este tipo de abertura toma exactamente el valor de los 90°.

c.-) Ángulo Obtuso, para este tipo de abertura su medida pueda variar desde los 90° hasta los 180° pero sin tomar tales valores, es decir, 90°<α<180°.

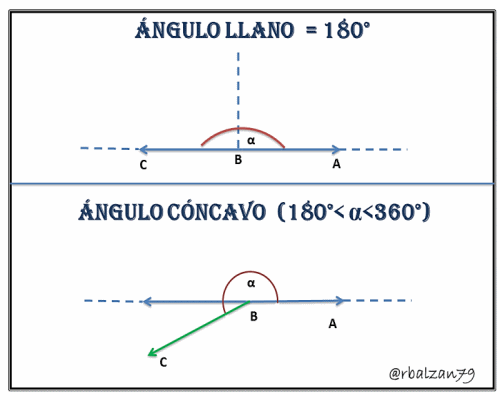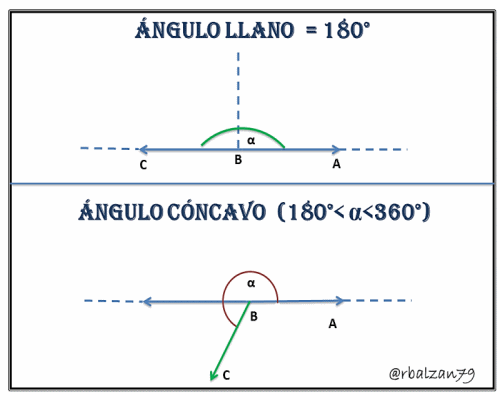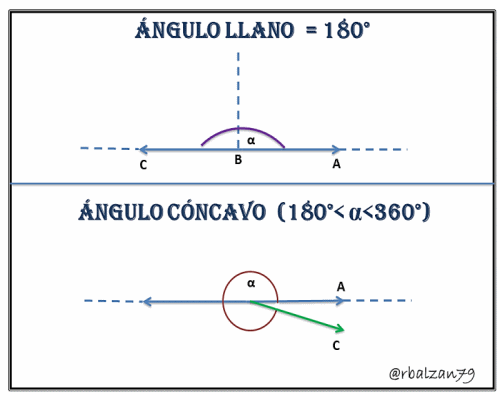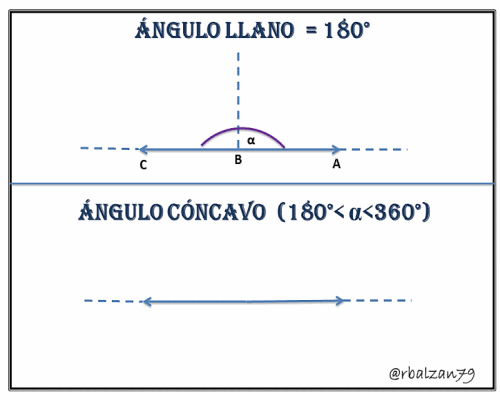
3.- Ángulo Llano, estas aberturas toman valores exactos a los 180°.

4.- Ángulo Cóncavo (No convexo), son aberturas cuyas medidas de arcos se encuentran entre los 180°<α<360°.

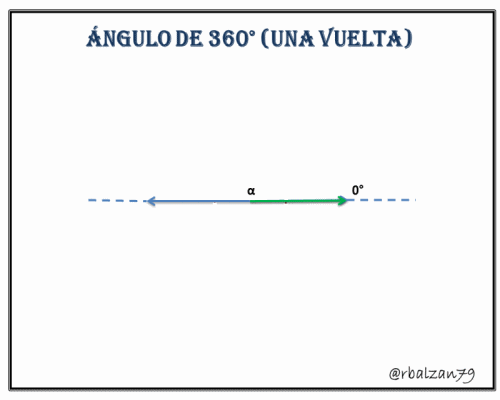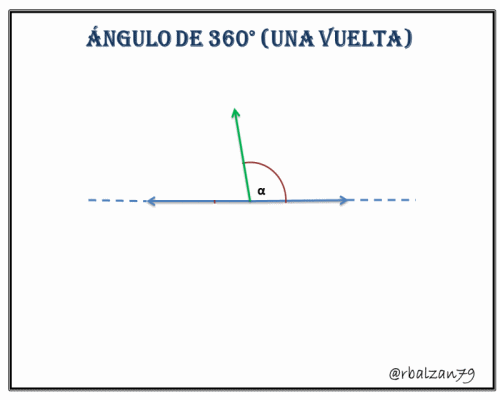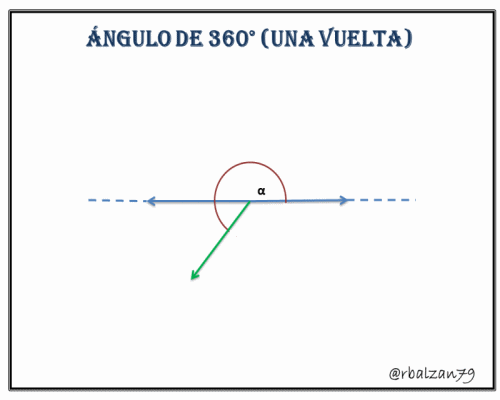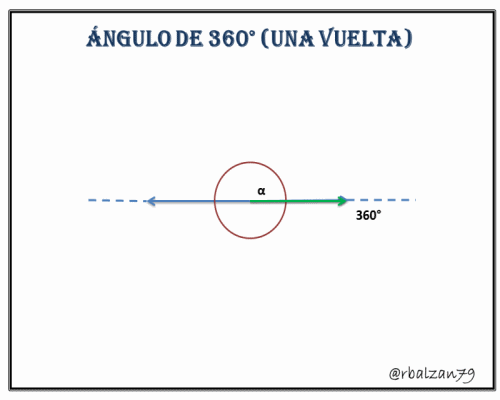
5.- Ángulo de 360° o de una vuelta, para el sistema sexagesimal representa la longitud total de una determinada circunferencia.

Una vez conocidas las anteriores aberturas podemos considerar los siguientes ángulos:

6.- Ángulos complementarios, está determinado por dos ángulos cuya suma será igual a los 90°, es decir, a un ángulo recto.

7.- Ángulos Suplementarios, el mismo está determinado por dos ángulos los cuales deben sumar 180°.

8.- Ángulos Conjugados, es aquel cuya suma de dos ángulos debe ser igual a 360°.

9.- Ángulos internos y externos, los cuales se originan por un par de rectas cortadas por una tercera recta.

Pendiente de una recta:

Una vez conocido el aspecto conceptual y analítico de la definición del ángulo, es importante considerar el estudio a mayor profundidad de la pendiente de una recta, debido a su importante cohesión con los ángulos y a lo que en nuestro desarrollo cotidiano e intelectual representan tales conceptos, en la publicación anterior utilizamos el termino de pendiente para hacer énfasis a las funciones afines y lineales en un plano, es decir, el estudio de una recta en el plano, en donde en la formulación algebraica de tales funciones la pendiente estaba presente como elemento esencial en el comportamiento direccional de tal línea recta en un determinado plano.

Para seguir complementando, podemos decir que la pendiente a la cual también llamamos acertadamente coeficiente angular no es más que la tangente de su ángulo de inclinación, ya hemos descrito a la letra (m) como el símbolo utilizado para representar dicha tangente, de igual forma la relación en donde m = tgα, en esta oportunidad una vez conocido el concepto de ángulo podemos notar con mayor facilidad el comportamiento de una línea recta en cuanto a su inclinación debido a que la misma estará vinculada a su abertura con respecto a un determinado plano.

Si observamos la figura 3, antes descrita en la definición de ángulos, en donde se encuentra las rectas t y t´ podemos decir que para ambos casos la pendiente podrá tomar todos los valores o números reales, en el caso cuando el ángulo (β) sea agudo, y ya hemos conocido este tipo de ángulo convexo, dicho coeficiente angular (pendiente) será positiva, esto representa el caso de la recta (t) y para el caso de un abertura o ángulo (β´) la pendiente o coeficiente angular será negativa como es el caso de la recta t´.

Recordemos que para poder calcular la pendiente de una recta conociendo dos puntos de la misma P1(X1 , Y1) y P2(X2 , Y2) la fórmula es la siguiente:

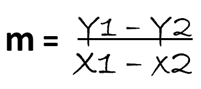
En la siguiente figura en la que los puntos P1P2 determinan una recta y en donde su ángulo de inclinación está determinada por (β) podemos trazar dos perpendiculares al eje de la X las cuales serán P1A y P2B, y también por el punto P2 tracemos una paralela al eje de la X la cual corte a P1A en un punto que llamaremos C, de esta manera obtenemos un triángulo rectángulo cuyo ángulo <P1P2C = β, entonces podemos decir, que ya conocemos que por trigonometría tenemos lo siguiente:

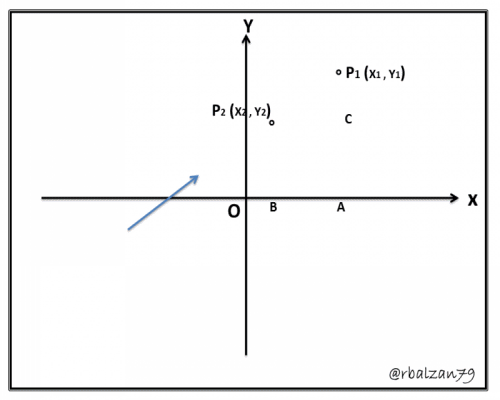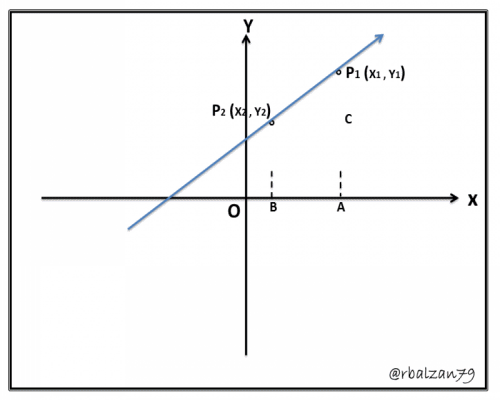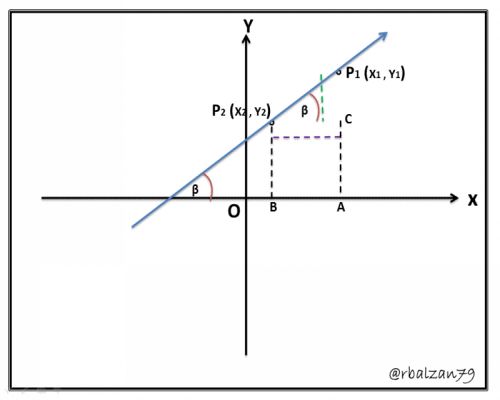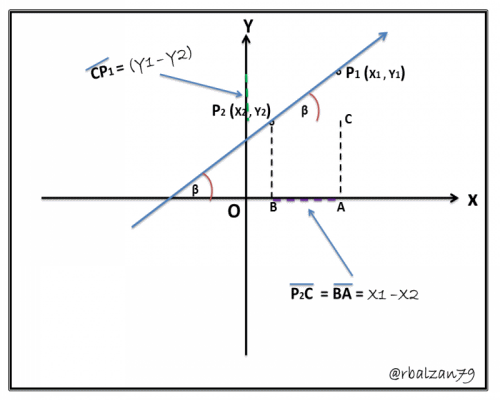
Por lo tanto, las coordenadas de cada uno de los puntos involucrados en la comprobación de la ecuación (1) son las siguientes:

A(x1 , 0) ; B(x2 , 0) ; C(x1 , y1) ; entonces tenemos:

CP1 = y1 – y2 ; P2C= BA= x1 - x2 ; y con esto verificamos la ecuación (1).

Conclusiones:

1.- Una de los aspecto más difícil de transferir hacia los estudiantes es sin dudas el carácter analítico hacia el estudio de cualquier figura geometría en particular, pero en forma global las transferencias de las matemáticas resulta una de las más complejas tareas a cualquier nivel educativo, creo que muchos docentes realizan grandes esfuerzos al aprovechar el carácter de cotidianidad de la cual goza esta magnífica ciencia geométrica, mi experiencia me ha llevado a decir que cuando el conocimiento lo empezamos a construir desde las bases ladrillo a ladrillo, es decir, paso a paso podemos ir cambiando la percepción de dificultad de los estudiantes hacia las matemáticas, un claro ejemplo de poco apasionamiento del estudiante está referido al hecho de establecer una demostración de un determinado conocimiento, creo que como estudiante lo pudimos vivir debido a que en ocasiones algunas de nuestras debilidades no fueron atendidas adecuadamente por el profesor, es por eso que siempre es importante pensar a través de nuestros estudiantes ya que nosotros pasamos por esa etapa, y a veces creemos conveniente no repasar algún conocimiento que previamente debería tener nuestros estudiantes con la finalidad de ganar tiempo, y lo que en muchas ocasiones logramos es que el estudiante se bloquee y pierda el interés por la obtención del nuevo aprendizaje ya que aún no tiene claro un determinado conocimiento base.

2.- La profundización en cuanto al entendimiento de ese elemento geométrico tan importante como lo es el punto, representa para nuestro entendimiento el eslabón necesario para poder adquirir cualquier tipo de aprendizaje en el mundo de las matemáticas a cualquier nivel académico, podríamos decir que el punto representa el átomo de la sustancia elemental de la geometría y que gracias a la geometría analítica plana ha adquirido mayor relevancia el estudio de dicho elemento geométrico, por lo tanto, decir punto es sinónimo de entendimiento geométrico de las distintas figuras en cualquiera de las dimensiones en las que se analice dichas figuras.

3.- La adecuada sincronización de los conocimientos previos con los adquiridos durante el desarrollo de una determinada cátedra siempre jugaran un importantísimo papel en el éxito en cuanto a la obtención de un determinado aprendizaje matemático, este aspecto debemos recordarlo siempre, ya que los conocimientos elementales o básicos de las matemáticas les brindara a nuestros estudiantes la confianza necesaria para el dominio y comprensión de nuevos saberes, hemos observado en el desarrollo de esta publicación la utilización de herramienta básicas (teorema de Pitágoras) para la demostración o comprobación de una determinada expresión algebraica llamada también fórmula o ecuación, la cual es aplicable en forma general a un conjunto de planteamientos matemáticos que guarden relación a dicha formulación.

4.- El concepto de ángulo el cual hemos descrito anteriormente, ha representado para la humanidad una importantísima herramienta matemática cuyo alcance se pierde de vista, debido a que gracias a la geometría analítica plana inicialmente ha reforzado dicho concepto ampliándolo y otorgándole mayores aspectos y capacidad de estudios prácticos a estas aberturas tanto entre dos rectas dirigidas como entre figuras geométricas, ya que por medio de varios sistema de medición le hemos podido dar carácter de proporcionalidad a los ángulos, entre el más reconocido por nosotros y nuestros estudiantes se encuentran el sexagesimal.

La utilidad del ángulo para el desarrollo modernista de nuestras sociedades ha sido muy destacada ya que ha servido de inspiración para grandes profesionales en distintas áreas como la ingeniería, arquitectura y en el propio campo académico de las matemáticas por nombrar algunas, ya que al igual que cualquier concepto geométrico aumenta y consolidad nuestro intelecto a cualquier nivel de nuestras vidas.

Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point 2010 y Photoscape.

Referencias Bibliográficas:

• Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

• Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

• Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

Autor: @rbalzan79