Sharding: How Many Shards Are Safe?
The trade-off between maximizing performance without compromising security.
Sharding is one of the most promising means of scaling distributed ledgers.
The concept behind sharding is simple: instead of requiring that every transaction pass through a single pool of validators, the network validators can be divided up into subgroups called shards, and each transaction must only pass through one of the shards. This is a powerful idea that allows the network to scale with the number of validators.
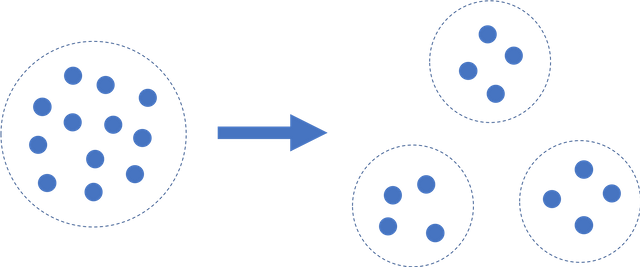 Sharding divides the network into distinct validation subgroups, which means only a fraction have to approve each transaction rather than the majority of all validators.
Sharding divides the network into distinct validation subgroups, which means only a fraction have to approve each transaction rather than the majority of all validators.
However, sharding introduces a new risk. In order for the network to be safe for all users, all shards need to satisfy the Byzantine validator limit, or the maximum percentage of validators that can act in a malicious or arbitrary manner.
In most networks, this limit is ⅓ of validators; beyond that limit, a consensus instance is fundamentally unsafe. Even if the validator set as a whole falls well under the limit, a single shard could be compromised. For instance, if a network with 10% Byzantine validators is split evenly into 10 shards and half the Byzantine validators end up in one shard, that shard will be 50% Byzantine and thus the entire network will be unsafe. This is known as a single shard takeover attack.
To address this problem, it is critical for the network to randomly assign validators to shards in a way that cannot be gamed (e.g. via a verifiable random function) and to ensure that the validator voting power is sufficiently uniform (e.g. via caps) so that they can be neatly divided into shards. These topics are fascinating but beyond the scope of this article. For now, we assume that both these properties are true, namely that equally weighted validators are assigned to shards randomly. We also assume that we distribute all of the validators to shards, which, as explained below, is important because it ensures the maximum amount of economic power is securing the network.
The key question, then, is how many shards can the network support?
Ideally, we would have as many as possible to maximize throughput. Note that sharding isn’t infinitely scalable due to inherent overhead, but, in general, the more shards the better. Ethereum, for example, is projecting sharding can yield 100–1000x scalability gains, which would correspond to similar numbers of shards. But performance is clearly secondary in importance to safety — a million TPS are of no use if they can’t be trusted!
This question is fundamentally a statistical one. Unfortunately, every sharding specification that I have seen, including those proposed by Ethereum, Dfinity, and Zilliqa, has used faulty statistical assumptions that can seriously compromise the security of the sharded network.
In this article, we will give an overview of why this is a risk and show how we can correctly analyze this risk.
The Tradeoff: Performance vs Security
Intuitively, for a given number of validators, the more shards there are, the greater the risk that any single shard is compromised. For example, if 10 of your 100 validators are Byzantine, a sharding scheme with 2 shards cannot be compromised since the max Byzantine percentage in either shard is 20% (10/50). At the other extreme, if you have 100 shards of 1 validator each, we know that 10 shards will definitely be compromised. This is the fundamental tradeoff at play: performance vs security.
Let’s first think about some more limits. To do so, we parameterize the problem with N validators, K of which are Byzantine, and a Byzantine limit of ɑ. The fraction of all validators that are Byzantine is p = K/N. We divide the entire set N of validators into S shards, with n = N/S validators assigned to each shard.
If p is close to ɑ, then for any non-trivial number of shards, there will almost certainly be a compromised shard. Conversely, if p is close to 0, then S can be correspondingly large.
The number of validators per shard, n, should be large enough to reduce the risk of a single validator tipping the balance one way or another. Similarly, N should be large enough to reduce this type of “chunkiness”.
If we know the probability of one or more shards failing per sharding round, P(F), we can then quantify the security of the network. Specifically, the average years to failure is equal to the expected number of sharding rounds until failure divided by the number of sharding rounds per year. Except for trivial cases, there will always be a non-zero chance that a shard will be compromised, but we can make this risk level reasonable. A network that fails, on average, once every 1000 years has an acceptable high level of security, while one that is expected to fail once a year is not secure enough.
The key question now becomes how to estimate P(F). It is here that other sharding specs fall short.
Statistical modeling of sharding
It turns out that this problem can be analyzed using standard statistics. Sampling in sharding matches the hypergeometric distribution, which describes the probability of k successes (Byzantine validators) out of n draws without replacement from a finite population of size N with K total successes.
Note that this matches our exact parameterization in the previous section for the first shard — a “success” is drawing a Byzantine validator, and we want to know the probability that after n draws we have fewer than ɑ*n Byzantine validators in a shard.
But what happens after the first shard?
We will have sampled n validators from the pool, and let’s say k1 are Byzantine. Then we have a new finite population of size N — n and K — k1 Byzantine validators remaining. After i shards sampled, there are N — i*n total validators and K — (k1 + k2 + … + ki) Byzantine validators left. `It is clear that the distribution parameters change significantly as we continue to sample, and that we cannot just use the base distribution to estimate the probabilities of the number of Byzantine validators for all shards.
This exact parameterization is not well studied, and existing generalizations like the multivariate hypergeometric distribution do not exactly correspond to our problem, so we have to do a bit of work to calculate the probability of at least one shard failure.
Error 1: The Binomial Approximation
What almost everyone does when presented with this problem is turn to the binomial approximation of the hypergeometric distribution. The binomial distribution describes the probability of k successes out of n draws with replacement where the probability of success for each draw is p. Using p = K/N, the global Byzantine fraction defined above, we can see that this matches the hypergeometric distribution, with the difference that samples are with replacement rather than without replacement.
It turns out the binomial approximation is pretty inaccurate for this problem. The binomial distribution is only a good approximation for the hypergeometric distribution if (1) N and K are large compared to n and (2) p is not close to 0 or 1. This makes sense. Let’s say you are analyzing the number of left handed people in a 10 person sample drawn from a population. The probability that the next person sampled is left handed is relatively constant if you are sampling from the population of a major city, so p does not change much from sample to sample. Conversely, if you are sampling from a group of 15 friends, of which 3 are left handed, p will change significantly on each successive draw. Neither condition can be assumed to be true for a robust sharding scheme.
A strong sharding scheme requires that you sample most, if not all, of the validators, meaning that n is close to N. In other words, it is not sufficient to only sample a small portion of the population. Doing so requires that you either dramatically expand the population of validators or you limit the number of shards to well below max capacity. The former dilutes the quality of the validators overall, while the later limits potential performance. Both make it easier for a Byzantine validator with a given fraction of the voting power in the network to have a large influence by random chance since you are only sampling a small portion of voting power.
Using an approximation like the binomial distribution requires justification, and clearly, these compromises are unacceptable since they reduce the economic power directly securing the network.
Thus, the binomial distribution is not a good estimate for the probability of a failure in sharding. It also is not a conservative upper bound, as it may give bigger or smaller estimates than the correct hypergeometric distribution. As a consequence, the security guarantees and assumptions of networks using this faulty assumption are potentially compromised.
Projects that use the faulty binomial approximation
Unfortunately, using the binomial distribution (and its CDF, i.e. “cumulative binomial”) is very common in sharding schemes, even those that assume the entire validator set is sampled.
Most notably, the Ethereum team has repeatedly used the binomial to describe sampling without replacement.
Vlad Zamfir
Ethereum sharding overview
Vitalik Buterin’s scalability paper
The team behind the theoretical Byzcoin and OmniLedger specs as well as the related Elastico also fall into this trap when estimating both committee selection and sharding probabilities, as do their derivative projects, such as Zilliqa.
Cardano uses the binomial approximation liberally, most notably for committee selection done without replacement. Even though they apply a conservative Chernoff bound, this bound is not accurate for the true hypergeometric distribution. Others that incorrectly assume sampling with replacement are Multichain and CryptoTask.
Error 2: Not Fully Sampling
The second (and more serious) major error comes from assuming that the probability distribution of failure in the first shard (or group) is indicative of the probability distribution of failure in any shard (or group). In other words, they assume the following equality:
P(failure in shard 1) = P(at least one failure across all shards)
It is readily apparent that this is fallacious. The probability of failure in any shard is clearly a function of the number of shards. For example, if failure is seeing tails on a coin flip, then the probability of at least one failure grows with each coin flip. Incidentally, this is the logic that underlies the binomial distribution itself!
In fact, all the examples from the previous section also make this error. If the probability of failure for any shard is p_f and independent (which is what the erroneous binomial assumption requires), then the probability of failure across all S samples is:
P(at least one failure) = 1-(1-p_f)^S ≥ p_f
This is an issue even if a project does not commit the first error and correctly uses the hypergeometric distribution. Unlike the binomial, successive hypergeometric samples are not independent. There are significant changes in the various parameters from the first to the second to the nth shard, which means that the inaccuracy of the estimate grows as the number of shards grows. This assumption leads to two sources of error relative to the true distribution!
For example, Dfinity’s white paper outlines that their system divides replicas (nodes) into disjoint groups G, and a defined security assumption is that each group is honest. This context is slightly different from sharding but has an equivalent security analysis. They then solve for the minimal group size (inverse of number of groups) using the cumulative hypergeometric distribution (i.e. CDF) for the first group. The RapidChain paper (written partly by Dfinity researchers) makes the same error in its epoch security analysis.
While this laxity is acceptable in the theoretical realm where developing a rough intuition of the number of nodes required is sufficient, it is a serious risk for practical deployment. A public decentralized network needs a deterministic way of setting the number of shards as a function of the number of nodes that changes dynamically over time, and the precision of this calculation has a big impact on the network’s practical security.
Example: Ethereum
In their sharding overview, Ethereum outlines their risk calculation and reports some failure probabilities. They conclude that sharding should be safe provided that the number of nodes per shard is at least 150 if sampling from a large population (i.e. assuming the binomial approximation is accurate).
Let’s assume for now that the binomial approximation is indeed appropriate and focus on the impact of the second error of not fully sampling.
For this example, we sample 150 nodes from an infinite population (i.e. with replacement — the incorrect assumption) that is 40% Byzantine with a per-shard Byzantine limit of 50% — exactly the Ethereum assumptions for the (1,3) entry of their probability table. The samples are independent since we are assuming for this example that sampling is done with replacement. The probability that the first (or any other) shard violates the limit is 0.82%. This matches the probability reported in the Ethereum sharding overview. But for 10 shards, the probability that any one is compromised rises to 7.96%. For 100 shards, it is 56.41%!
Admittedly, the probability given by Ethereum is for the first shard. But the clarifying footnote claims that it is indeed equivalent (or at least roughly so) to the probability for all shards:
The probabilities given are for one single shard; however, the random seed affects O(c) shards and the attacker could potentially take over any one of them. If we want to look at O(c) shards simultaneously, then there are two cases. First, if the grinding process is computationally bounded, then this fact does not change the calculus at all, as even though there are now O(c) chances of success per round, checking success takes O(c) times as much work. Second, if the grinding process is economically bounded, then this indeed calls for somewhat higher safety factors (increasing N by 10–20 should be sufficient) although it’s important to note that the goal of an attacker in a profit-motivated manipulation attack is to increase their participation across all shards in any case, and so that is the case that we are already investigating.
Increasing the sample size (N in the Ethereum page) by 20 only decreases the probability of failure with 10 shards to 5.09% and with 100 shards to 40.71%, still obviously unacceptable. This is not even accounting for the error from incorrectly assuming a binomial rather than hypergeometric distribution!
Correctly Calculating Failure Probability
(Math warning. You can safely skip to the next section if you prefer not to see how the sausage is made!)
There are a few approaches that we can take to calculate the probability that at least one shard has a failure. Which one is better will depend on the exact input parameters.
Statistics: Using the Hypergeometric Distribution
Repeating the parameterization given previously, we have N validators, K of which are Byzantine, S shards, and a Byzantine limit of ɑ. The fraction of all validators that are Byzantine is p = K/N. We divide the entire set N of validators into shards, with n = N/S validators assigned to each shard. Shard i has ki Byzantine nodes such that (k1 + k2 + … + kS) = K, and Xi is the random variable taking values ki.
Let H(N,K,n) be a hypergeometric distribution corresponding to the first shard sample. That is,
X1 ~ H(N, K, n)
But the distribution changes for the second shard. Specifically, we need to incorporate the information from k1 in the distribution of k2:
X2 ~ H(N-n, K-k1, n)
For the ith shard, the distribution is:
Xi ~ H(N-(i-1)*n, K -(k1 + … + k(i-1)), n)
Jointly, the Xi have the following distribution:
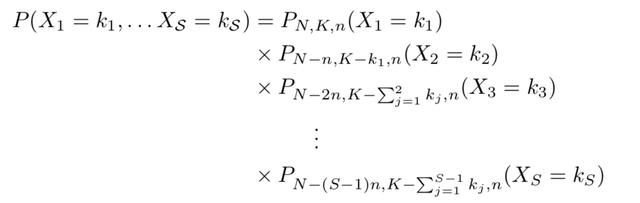
Where P_{N, K, n} is the probability of a random variable outcome corresponding to H(N, K, n):
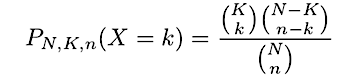
The hypergeometric probability has the following intuitive explanation: first pick k successes out of K total successes, then pick n — k failures out of N — K total failures. The number of ways to pick each is given by the binomial coefficients C(K, k) and C(N-K, n-k). The total number of ways to pick a sample of size k + (n-k) = n is given by C(N,n).
Substituting in this probability and going through some tedious algebra yields the full joint distribution:
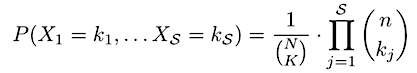
Intuitively, we can think of this single particular outcome as one out of all possible total outcomes. The total number of outcomes can be thought of as the lining up N-K non-Byzantine nodes and placing K Byzantine nodes among them (including at the beginning and end). Alternatively, we have N total slots and need to pick K of them for the Byzantine nodes. The number of possible resulting orders is equal to C(N, K). Then, the first n nodes in the resulting line up are assigned to the first shard, the second n to the second shard, and so on. Since order does not matter within each shard, we have to divide by the number of ways to arrange k_j Byzantine nodes and n — k_j non-Byzantine nodes in shard j, which is equal to C(n,k_j) by the same result. The probability is then the inverse of the total number of total distinct outcomes. It is easy to verify that this is a proper PDF that sums to 1 by simplifying the product using the generalized version of Vandermonde’s identity.
We can use the probability for a particular outcome to get the probability of all safe outcomes using the joint CDF:
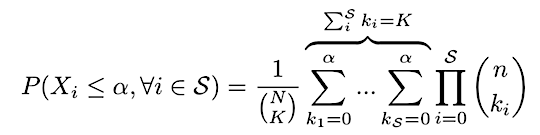
This is derived by summing over all outcomes where none of the k_j exceed the shard security threshold ɑ, which in our case is ⅓*n.
This probability distribution is still somewhat nasty, which is, of course, why most people default to the binomial approximation. Unfortunately, a closed-form simplification, which is required to solve analytically for a target hazard rate, is difficult to achieve.
We can directly sum over all possible values of the k_j’s using a statistical package, but this quickly becomes intractable for large values of N, K, and S. While impractical in most cases, the insights from this derivation can help us directly calculate the probability using generating functions.
Generating Functions and Combinatorics
Generating functions are a convenient way to count scenarios with constraints encoded. In this case, we have S shards, each that will be assigned n validators with a Byzantine limit of ɑ = ⅓*n. We need to divide K Byzantine validators between these shards without exceeding the limit.
This corresponds to the following generating function for a single shard:
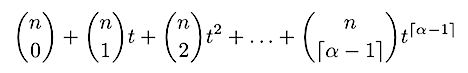
Or, equivalently:
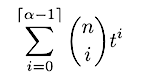
This generating function counts the number of ways we can construct a single shard from the pool of validators under these constraints. The coefficients of each t^i indicate the number of ways that a shard can have i Byzantine nodes. We stop at t^(ɑ — 1) since that is the maximum number of Byzantine nodes allowed (the limit is a strict inequality).
To get the total number of ways we can distribute the K Byzantine validators across all S shards, we then simply multiply this polynomial with itself S times:
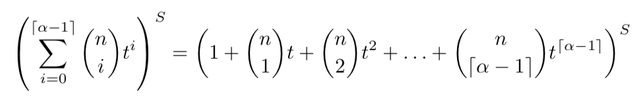
and extract the coefficient of t^K.
The total number of possible outcomes is C(N,K) per the logic in the last section, so the desired probability is then:
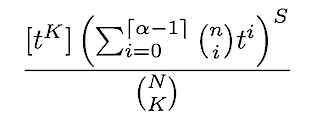
By reframing the problem in the context of generating functions, we are iterating over the number of shards rather than the number of possible combinations of k_j. This ends up being easier to solve computationally.
The coefficients of the expanded polynomial can be solved analytically according to the multinomial theorem, which recovers a form that looks similar to the CDF we just found. It is easier, however, to simply use a symbolic math system to compute these coefficients in the most efficient way. Here is an example using Wolfram Alpha, while the Python script I uploaded uses the Sympy package.
The generating function approach is the easiest way to directly compute the probability of failure in any shard.
Simulation
While more efficient than the raw statistical calculation, computing for polynomial coefficients gets intensive for large values. While less elegant, simulation can make the problem tractable.
Direct simulation in this case is quite simple, simply requiring many trials of fully sampling for all shards. The key is to do this without replacement. Simulation has the added benefit of allowing the easy testing of more complex problem formulations, such as validators having non-equal weights or dependent behavior.
An interesting question is how we know we have run sufficient simulations. The easiest way to answer this question is to use a confidence interval for the proportion of simulations that fail. Provided that the top end of the confidence interval (using a relatively wide confidence level) is below our maximum risk level, we can be confident the tested sharding parameters will be safe.
Note that the number of samples required grows quite quickly as the probability of failure approaches zero. However, for probabilities around 1e-6 or greater (corresponding to more than 1000 years to failure, assuming one sharding round per day), it is quite easily computed on a laptop, while smaller probabilities can be computed in parallel on larger hardware like AWS.
Mathematical Bounds
When simulation is impractical, an alternative methodology would be using mathematical bounds on the success probability. The Chernoff bound is typically the sharpest, but requires that the variables of interest be independent (not true here). The looser Markov and Chebyshev bounds do not have the same requirement and are more useful in this context.
While the number of shards is less than 10,000 or so, simulation is still the best solution. As we will see below, it is unlikely that we will see this number of shards (or anywhere close) anytime soon.
Putting it together: how many shards are safe?
I have uploaded a simple Python script that calculates sharding failure rate, with options for either computing it analytically using generating functions or via simulation. It calculates the probability both with replacement (binomial assumption) and without (true hypergeometric) replacement to measure the effect of the first error. It also calculates the probability if you make the second error and only use the first shard.
There is no single answer for how many shards a network can have. The exact answer is a function of multiple parameters: how many total nodes, the assumed Byzantine percentage, and the risk tolerance of the network.
Rather than determining the number of shards based on a strict formula shared by all nodes, it makes most sense to have some sort of decentralized governance mechanism that allows nodes to come to consensus on the number of shards. This allows nodes to reflect their own independent calculations, which may incorporate more sophisticated information and criteria, as well as their own risk tolerance.
What might this calculation look like for a reasonable network state? Let’s assume we have N = 1000 robust network validators, with K = 150 (i.e. 15% of validators are Byzantine) and a Byzantine limit of ⅓. A reasonable mean time to failure that minimizes risk while not throttling performance is 500 years. Can this network support S = 10 shards?
The table below shows the various analytical probabilities calculated correctly under the various ranges of methodologies used in sharding specs. The top left is the correct probability (hypergeometric for the full sample), while the other three demonstrate different combinations of the two errors: using the binomial approximation or only the first shard.

The failure rate given by the binomial assumption is 1.84e-5, while the failure rate given by the true hypergeometric distribution is 3.72e-6, a five times difference! Assuming one sharding round per day, the true mean time to failure is almost 750 years, comfortably above our goal of 500 years.
The binomial assumption, however, would lead us to believe that mean time to failure is less than 150 years, an unacceptable risk. In this particular example, the binomial assumption leads to a conservative estimate and merely suboptimal performance, but this is not guaranteed to be true.
On the other hand, only using the first shard probability underestimates risk by a factor of 10!¹ While not a risk here, the example from before shows that this can have a disastrous impact on safety.
1000 Shards: A realistic possibility?
Since the number of advisable shards is so dependent on the parameters, a key question in this analysis is what parameters are reasonable. A good example is Ethereum, which has a stated goal of 1000 or more shards.²
There are substantial non-security issues, such as overhead, that likely will produce a Laffer Curve type relationship where adding additional shards decreases throughput. We will ignore these considerations for now and focus purely on security.
Ethereum estimates they need 150 validators per shard to be safe. This corresponds to 150,000 validators for 1000 shards.
Running this through the simulator assuming 33% of nodes are Byzantine with a BFT limit of 50% shows that correctly sampling without replacement for all shards has a failure probability of 5.94e-3, which is quite large.
However, the Ethereum page claims that the failure rate for N=150 assuming 33% Byzantine validators is 1.83e-5. This means that the true failure probability is 325 times what the Ethereum spec believes! Put another way, the Ethereum probability indicates a mean years to failure of 150 (not horrible), but the true mean years to failure is 0.46 — less than half a year! The security implications of such a poor approximation are self-evident.
Given an arbitrarily large number of validators, of course, any finite number of shards can be supported theoretically. But how reasonable are the assumptions behind this logic? Validator power will almost certainly follow some sort of skewed distribution like a Pareto, reflecting the natural distribution of economic power in systems. With 150,000 validators, a network would have a massive left tail, where the first few hundred validators have more power than all other validators combined.
You have two options to address this outcome. If you weight by voting power, then you end up with far fewer effective validators. If you do not weight, then you end with shards that have a massive deficiency in economic value securing that shard. This would make validators in that shard have disproportionate power in the network than their economic contributions to the network justify. This in turn makes the network more susceptible to bribing attacks. In other words, a huge number of validators increases the posterior probability that validators become Byzantine.
This means that the assumptions of the sharding probability estimates, in particular that the Byzantine validators are fixed, that are reasonable for a moderate number of nodes do not hold for a huge number of nodes and a large number of shards, such as 1000.
It is important for sharding specs to recognize the limits of these assumptions and sufficiently incorporate metrics reflecting economic value securing each shard. It also highlights the importance of having a sufficiently scalable and performant unsharded network, as sharding alone cannot arbitrarily increase capacity.
Why does any of this matter?
The most empowering feature of DLT is that it is trustless, meaning you do not need to trust in any counterparty; instead, you trust the math and code behind the network.
The crucial assumption obviously is that you can trust the math behind the network. This is particularly important when considering a key safety question like how many shards are safe to use in a network. It is also not one that can be answered for a single set of network parameters; rather, it must be answered deterministically by decentralized nodes as the open network dynamically changes over time.
Relying on faulty mathematical and statistical approximations when answering this question can at worst lead to a critical security risk (if the approximation overestimates the number of shards) and suboptimal scalability (if the approximation underestimates the number of shards). The former makes the network unreliable, while the latter will manifest as additional cost to end users.
At Logos, we prioritize both theoretical and practical safety equally. These approximations may be acceptable in an abstract research paper, but in the real world, a single security breach is a game breaker.
With the flurry of credit card and payment hacks that plague retail and e-commerce around the holiday time, it’s of the utmost importance for us at Logos to allow consumers to make transactions without a second thought for the security of their money. Using proven mathematical calculations, we are able to accurately ensure that future Logos users will be guaranteed a safe and trusted way to pay.
[1] Due to the other binomial approximation.
[2] I focus on Ethereum for examples since they are the best-known project attempting sharding.
Hello @logos.network! This is a friendly reminder that you have 3000 Partiko Points unclaimed in your Partiko account!
Partiko is a fast and beautiful mobile app for Steem, and it’s the most popular Steem mobile app out there! Download Partiko using the link below and login using SteemConnect to claim your 3000 Partiko points! You can easily convert them into Steem token!
https://partiko.app/referral/partiko
Congratulations @logos.network! You received a personal award!
Click here to view your Board
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness and get one more award and increased upvotes!
Congratulations @logos.network! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!