Euclid’s Proposition 1:5
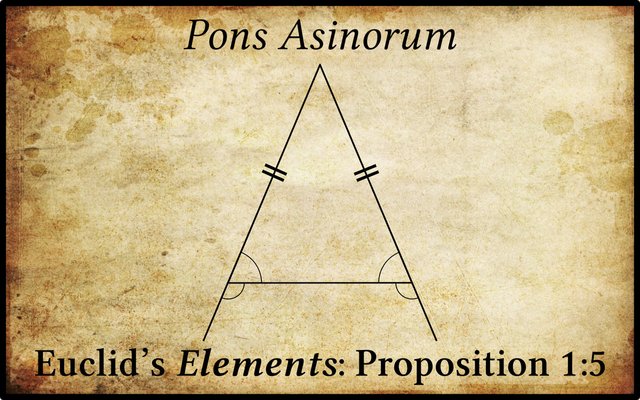
The fifth proposition of Book 1 of Euclid’s Elements proves two things about isosceles triangles. The first of these is probably the best known property of this type of triangle:
| Greek | English |
|---|---|
| Τῶν ἰσοσκελῶν τριγώνων αἱ τρὸς τῇ βάσει γωνίαι ἴσαι ἀλλήλαις εἰσίν, καὶ προσεκβληθεισῶν τῶν ἴσων εὐθειῶν αἱὑπὸ τὴν βάσιν γωνίαι ἴσαι ἀλλήλαις ἔσονται. | For isosceles triangles, the angles at the base are equal to one another, and if the equal sides are produced then the angles under the base will be equal to one another. |
According to Proclus, who wrote a commentary on the first book of the Elements, it was the Ionic philosopher Thales of Miletus who first discovered that the angles at the base of an isosceles triangle are equal to one another (Morrow 195).
The student might wonder why Euclid proves not only that the angles at the base of an isosceles triangle are equal to one another but also that the external angles beneath the base are equal to one another. Thomas Heath also wondered about this:
An interesting question arises as to the reason for Euclid’s insertion of the second part, to which, it will be observed, the converse proposition 1.6 has nothing corresponding. As a matter of fact, it is not necessary for any subsequent demonstration that is to be found in the original text of Euclid, but only for the interpolated second case of 1.7; and it was perhaps not unnatural that the undoubted genuineness of the second part of 1.5 convinced many editors that the second case of 1.7 must necessarily be Euclid’s also. Proclus’ explanation, which must apparently be the right one, is that the second part of 1.5 was inserted for the purpose of fore-arming the learner against a possible objection (ἔνστασις), as it was technically called, which might be raised to 1.7 as given in the text, with one case only. The objection would, as we have seen, take the specific ground that, as demonstrated, the theorem was not conclusive, since it did not cover all possible cases. From this point of view, the second part of 1.5 is useful not only for 1.7 but, according to Proclus, for 1.9 also. ―Heath 255 : Morrow 192–193
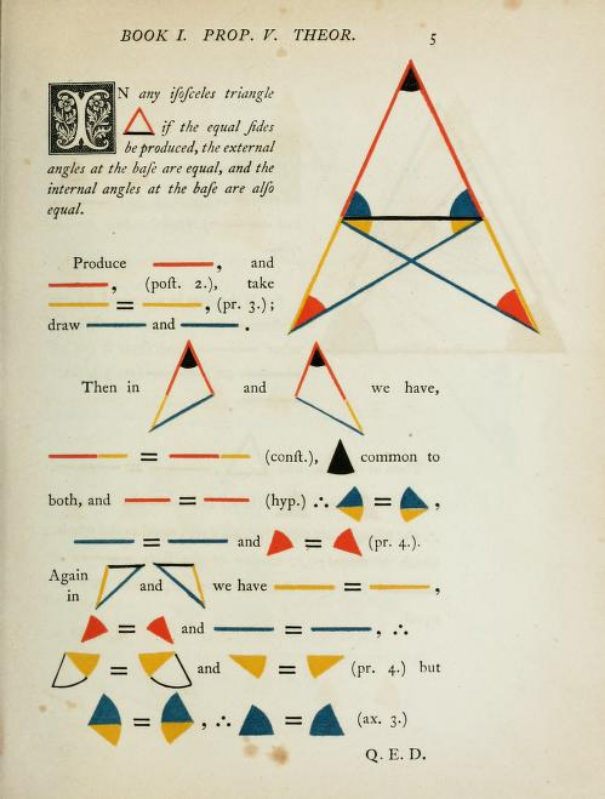
In this proposition Euclid makes use of the following definitions, postulates, common notions and propositions:
Definition 20 And of the trilateral figures: an equilateral triangle is that having three equal sides, an isosceles (triangle) that having only two equal sides, and a scalene (triangle) that having three unequal sides.
Postulate 1 Let it have been postulated to draw a straight-line from any point to any point.
Postulate 2 And to produce a finite straight-line continuously in a straight-line.
Common Notion 3 And if equal things are subtracted from equal things then the remainders are equal.
Proposition 1:3 For two given unequal straight-lines, to cut off from the greater a straight-line equal to the lesser.
Proposition 4 The Side-Angle-Side Congruence Theorem for Triangles. Euclid invokes this theorem twice in his proof.
In modern terms Euclid’s proof of this theorem may be expressed as follows:

Pons Asinorum
Proposition 1:5 is sometimes known as Pons Asinorum, or The Asses’ Bridge. The usual explanation is that the first four propositions in the Elements are easy to follow, but Proposition 1:5 represents a step-up in difficulty that all too often proves insurmountable for many students of geometry. Unable to cross this bridge, these donkeys give up and put down their Euclid. This explanation has been questioned, however. Others suggest that the diagram for this proposition resembles a hump-backed bridge which is too steep for a horse to cross but which an ass could traverse.
Originally, it seems, the term pons asinorum was applied to a mnemonic diagram devised by the Aristotelian commentator Alexander of Aphrodisias around 200 CE and reproduced in the 6th century by the Byzantine polymath John Philoponus. The device helped students of logic remember which types of conclusions followed from which types of premises, as explained by Aristotle in his Prior Analytics (Book 1, Chapters 27–29).
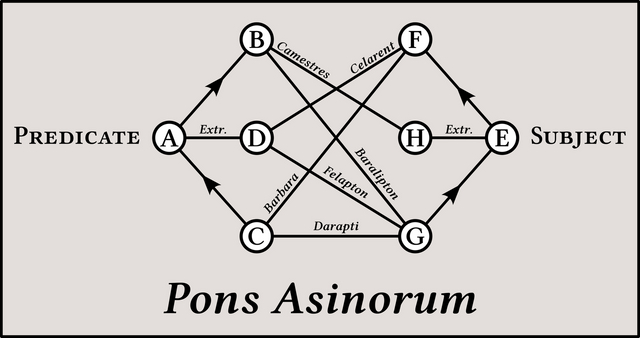
Similar devices were used by Scholastic philosophers in the Middle Ages to assist students of logic in finding the middle terms of syllogisms. The device continued to be employed as a teaching aid by Scotist philosophers―followers of the teachings of Duns Scotus―into the Renaissance. It is said that the French Scotist Pierre Tartaret, who taught at the University of Paris around 1500, was the first to call the device pons asinorum.
How the expression came to be applied to Euclid’s fifth proposition has been explained by the American philosopher of logic Charles Sanders Peirce, who traced this usage to Cambridge University around the time of the Protestant Reformation. In a letter to the New York Daily Tribune (Tuesday 6 January 1890) Peirce wrote:
But the true explanation of the phrase is to be sought in its much older application in logic, concerning which the curious may consult Bayle under Buridan, and Rabelais, Book II, chapter xxviii, last paragraph. Almost all terms of mediaeval logic are to be explained by passages of Aristotle. Now Aristotle (I Anal. post. 34) defines sagacity as a certain power of aiming well at middle terms of demonstrations; and this definition we find alleged as justification for assigning to a certain diagram designed to enable the fatuous, stupid and slow to place a middle term between two given extremes the name of pons asinorum.
Only Scotist treatises give this diagram; and after the Scotistic teaching had been forbidden in Cambridge by the royal injunctions of 1535, and Euclid had been prescribed as the initiatory study in 1549, the name pons asinorum (the original signification having been forgotten) became transferred to the geometrical theorem. It happens that the figure of the Fifth Proposition has some resemblance to a part of the logical diagram, but whether this really influenced the application of the phrase is mere matter of surmise. It is said that there is a difficulty in making donkeys cross a bridge. This would render the geometrical signification still more apt. The phrase pont aux ânes, in French, meaning a difficulty at which we are apt to halt, but which readily yields to a determined effort, accords with this. On the other hand, the German word Eselsbrücke, if I mistake not, means something to aid the uneducated. ―C S Peirce, New York Daily Tribune, 6 January 1890, Page 14 Column 5

It was around the same time (circa 1530) that students who persisted in the study of the Catholic theology of Duns Scotus rather than embracing the New Learning of Humanism and Protestant theology came to be known as dunces.
In France the Pythagorean Theorem (Proposition 1:47) is called Le pont aux ânes, a French translation of the Latin pons asinorum. In his Dictionnaire de la langue française Émile Littré explains this phrase as referring to something so easy and banal that everyone can understand it―which is the very opposite of the usual explanation given for Pons Asinorum.
Other Proofs
Euclid’s proof is quite involved and far from easy to follow without close attention to the diagram. But his was not the only proof of this important result.
In Book 1, Chapter 24, of his Prior Analytics Aristotle provides a proof of the first part of the theorem that differs significantly from the one in Euclid. Aristotle requires us to construct a circle with centre A and radius AB. As |AC| = |AB|, the point C will also lie on the circle and AC will also be a radius. As Thomas Heath notes, Aristotle’s proof relies on so-called mixed angles―an angle between a line and a curve. Here the mixed angles lie between the base of the triangle BC and the circumference of the circle. Apparently mixed angles played a much larger role in geometry before Euclid (Heath 252–253).
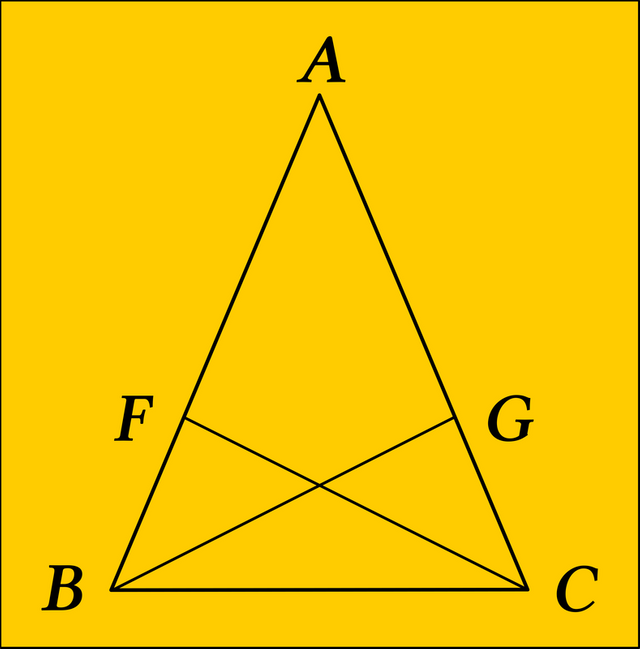
Proclus gives a proof of the first part of this theorem that does not require the sides of the triangle to be extended. It is essentially the same as Euclid’s proof, making use of the Side-Angle-Side Theorem twice to establish the congruence of smaller triangles. But Proclus places his point F between A and B. Once again, triangles ABG and ACF are congruent by Side-Angle-Side, as are triangles FBC and GCB:
Pappus of Alexandria, who flourished in the 4th century of the Common Era, has also provided us with an alternative proof of the first part of this theorem. It is shorter than Euclid’s, and quite ingenious, but conceptually more difficult for the beginner. Pappus points out that the Side-Angle-Side Theorem may also be applied directly to the isosceles triangle ABC to prove that this triangle is congruent to the triangle ACB, which shares the same vertices: |AC|=|AB|, and |AB| = |AC|, and ∠BAC = ∠CAB. Therefore all the corresponding angles are equal: ∠ABC = ∠ACB, and ∠ACB = ∠ABC.
Proposition 1:5 is one of the most useful theorems in the Elements. Euclid uses it to prove several propositions in Books I, II, III, IV, VI, and XIII.
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Oliver Byrne, The First Six Books of The Elements of Euclid in Which Coloured Diagrams and Symbols Are Used Instead of Letters for the Greater Ease of Learners, William Pickering, London (1847)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- C L Hamblin, An Improved Pons Asinorum? Journal of the History of Philosophy, Volume 14, Number 2, Pages 131–136, Johns Hopkins Hospital University Press, Baltimore, Maryland (1976)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Volume 1, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- C S Peirce, The Pons Asinorum Again: Mr Peirce Sets Forth the History of the Phrase from the Times of Duns Scotus’s Followers, New York Daily Tribune, Tuesday 6 January 1891, Page 14, Column 5 (1890)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
Image Credits
- Charles Sanders Peirce: Napoleon Sarony (photographer), New York Public Library, Public Domain
Online Resources
