The geometric mean and the arithmetic mean

In mathematics different kinds of means or averages are used. Among the most well known are the arithmetic and geometric means. The arithmetic mean is used by everybody in everyday tasks. However the geometric mean is less known by the general public. In the present post I will show the inequality that relates these two quantities, the geometrical mean is smaller than its arithmetic counterpart. Let a₁, …, a_n be positive numbers, we shall prove the following inequality

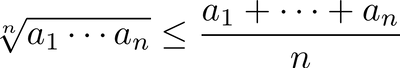
Moreover we have equality only in the case the the numbers a_i’s, for 1 ≤ i ≤ n, are all equal.

For example, the geometrical mean of 18 and 2 is (2•18)^1/2 = (36) ^1/2=6, whereas their arithmetic mean is (2+18)/2=10, clearly 6 < 10.

There are different ways to prove this inequality, some more ingenious than others. Today I will show an elementary and beautiful proof of this fact. It only involves elementary geometry; in fact, it only uses the Pythagoras Theorem.

Let a and b be positive numbers, such that 0<a<b. We consider segments of length a and b, respectively, and we arrange then in collinear and consecutive manner. Later we form a semi-circumference, whose diameter is a+b, as it is shown in the following figure:

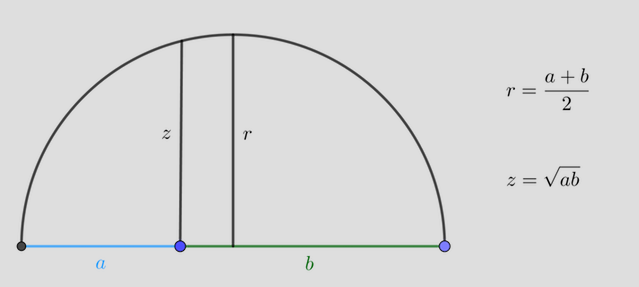
Let B the right end of the segment of length a and the left end of the cement of length b. From B we consider a perpendicular segment to the diameter; this segment goes from B to the intersection point to the circumference, i.e. the point O. We denote by z its length. Clearly z is less than the radius of the circumference, i.e. (a+b)/2. Keep in mind, that there is equality only in the case a=b. We shall show that z is the average mean of a and b.

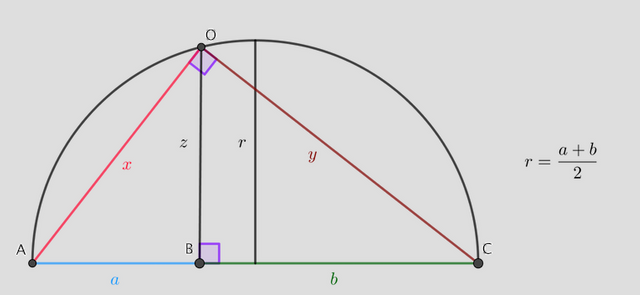
We consider the segments AO and OC, and their lengths are denoted by x and y, respectively.

Since the triangle AOC is a right triangle, by Pythagoras theorem we have x²+y²=(a+b)².
On the other hand the triangle OBC is also a right triangle, so, y²=b²+z².
Similarly, using Pythagoras theorem for the triangle ABO, we get: x²=a²+z².

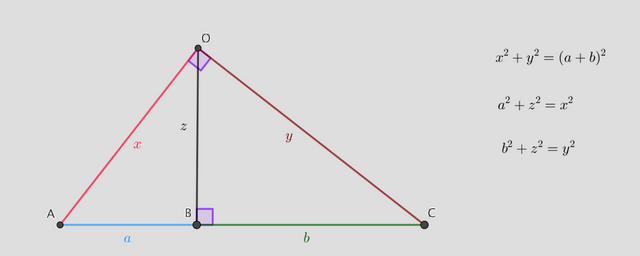
After comparing these identities, we conclude:

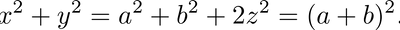
Therefore: z²=ab, i.e. z=(ab)^(1/2). In other words z is the geometrical mean of a and b. We generalize this inequality for n numbers, using induction. In this way, we obtained the desired result.

Reference:
R. Nelsen, Proofs without words, Exercises in visual thinking. MAA, 1993.

The figures in this post were done by myself using GeoGebra and the formulae were typed using LaTeX.