Wormholes
Who has watched Star Trek
or the more recent Interstellar 1,
has an ideia of what they are: shortcuts in spacetime that allow intrepid space explorers to cover vast distances in very little time, apparently connecting two distant regions of the universe, like in this two-dimensional representation below:
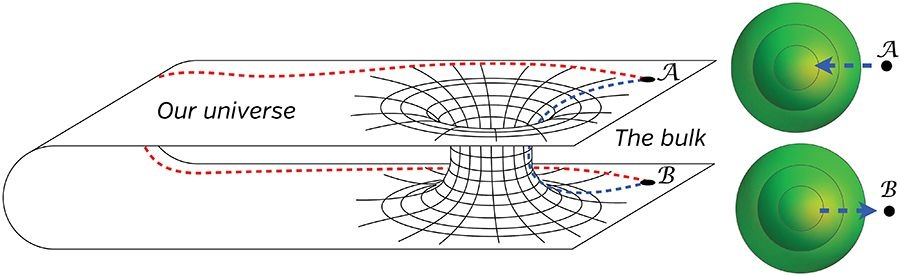
[Source: "The Science of Interstellar", de Kip Thorne]
The term wormhole was coined by John Wheeler, who was also the author of many curious names in gravitation physics, such as blackholes. In this case, he is referring to the tunnel a worm makes inside an apple, connecting to "distant" regions on the apple's surface:

[Source: "The Science of Interstellar", de Kip Thorne]
But do these things actually exist? Even better, let us try to answer a much simpler question: are these things possible? Well, the answer is at the end, so bear with me.
Karl Schwarzschild [1872-1916] was a german physicist and astronomer who became immediately known for publishing in 1916 a famous solution to the Einstein field equations. His solution describes the exterior gravitational field of a spherically symmetric body - like the gravitational field of our sun. The Schwarzschild solution, as it is called, is an exact solution of the Einstein equations in vacuum,
where typically (in four dimensions) the indices i and j take on the values 1,2 and 3 for the three spatial coordinates and the value 4 for the temporal coordinate. (Actually, in the physics literature, it is more common to assign the value 0 for the temporal coordinate).
These are the differential equations for the metric . Think of the metric as a symmetric 4x4 matrix whose components are infinitely differentiable functions of the coordinates used to describe spacetime.
What does the metric describe? A physicist will tell you it describes the geometry of spacetime, since if you know the metric, you can calculate the distance (in four dimensions) between two neighboring points.
To fix ideas, think of the cartesian system in two dimensions, described by the cartesian system of coordinates , with
being the horizontal axis and
being the vertical axis. A point in this system is described by a pair of numbers: its coordinates with respect to the horizontal and vertical axes. Suppose this point has the coordinates
. Then a very close point will have coordinates
, and the squared distance between these points, using the Pythagoras theorem, is
. It is common to represent this squared length as
. We could even represent this squared length in a lot more compact way, such as:
where we have used the metric to describe the length, and in this case it is a 2x2 matrix, because we are in a two-dimensional space. Comparing both expressions, you can check that this matrix is the 2x2 identity matrix:
Let us now go back to the Schwarzschild solution. As we now know, this solution is a spacetime metric, and it is written in the following form, in terms of the squared length,
In this expression, M is the mass of the spherical distribution of matter (the sun, for instance), and the metric is written in spherical coordinates, where r is the radial coordinate and represents the element of solid angle (the angular bit).
What is interesting to observe in this solution is that the function which multiplies the term becomes singular (the denominator vanishes) when r=0 or when r=2M. These singularities can be of great physical and mathematical importance, and in particular, in the Schwarzschild solution, the r=0 singularity is related to the existence of a blackhole solution (but this is something for another post). The singularity r=2M can be "removed", though, by using another coordinate system which extends the one initially adopted to describe the Schwarzschild metric. This extension is called the Kruskal extension, and it contains the Schwarzschild solution.
In order to represent these spacetimes (or solutions to the Einstein equations), one usually draws two-dimensional diagrams, where one ignores the angular part (due to symmetry). Thus, in the diagram in Kruskal coordinates below, each point has coordinats (T,X) and represents a two-dimensional sphere:
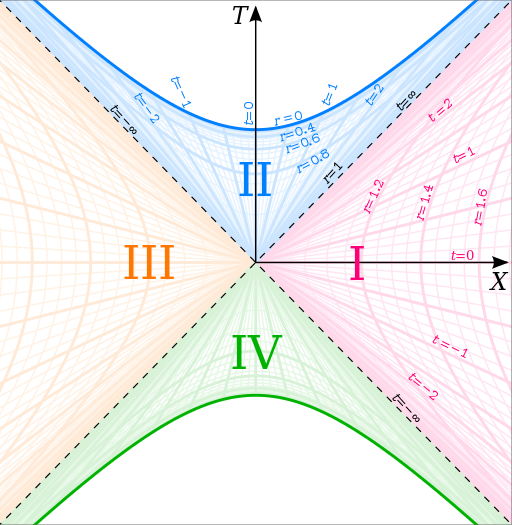
[Source:Wikipedia]
In the figure, the curve r=0 in blue is the singularity we mentioned earlier, and all straight lines at a 45 degree angle with the horizontal axis represent light beam trajectories. If we represent the spatial hypersurface T=0 (the X axis) as a two-dimensional surface embedded in three-dimensional flat space, it would have the shape
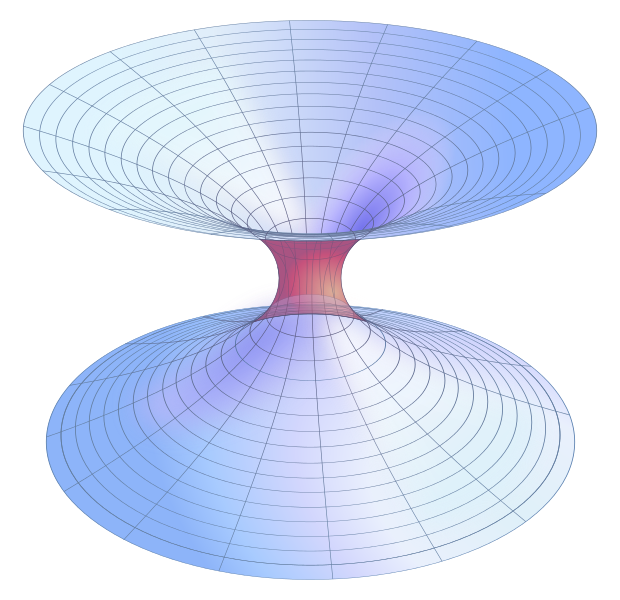
[Source:Wikipedia]
Here each circle is in fact a two-dimensional sphere (one coordinate is suppressed). The tunnel, or throat, connects the regions I and III of the Kruskal diagram, and it is called the Schwarzschild wormhole, or Einstein-Rosen bridge.
The lesson here is: are wormholes possible? Yes, if you accept that they are possible solutions of the Einstein field equations. However, there are complex issues to be considered, such as the stability of these structures, and if it is possible to traverse them in either direction. Have in mind that this is only a simple example, and there are complicated holes out there in scientific literature (see, for example, the references in 2).
At last, if you have come this far, here goes a cute short film, "Einstein-Rosen":
ps: since there is no native LaTeX support, I managed inserting equations with this workaround.
1Interstellar. As a matter of fact, this movie had the theoretical physicist and Nobel prize winner Kip Thorne as scientific advisor.
2 Wikipedia
Congratulations @fresneda! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Congratulations @fresneda! You received a personal award!
Click here to view your Board