Introducción a las Ecuaciones Diferenciales Parciales | Lección #4

Saludos queridos lectores, bienvenidos nuevamente. En esta oportunidad les traigo la 4^ta Lección de la serie Introducción a las Ecuaciones Diferenciales Parciales (EDP), en la misma desarrollaremos este tan importante e interesante tema, en donde podemos aprender algunos métodos para la resolución de estas ecuaciones así como muchas aplicaciones, sobre todo en el campo de la física, química, biología y otras ciencias, así como no podemos dejar de mencionar sus aplicaciones a la ingeniería y carreras afines. En la gama de problemas que se modelan con Ecuaciones Diferenciales Parciales, podemos mencionar algunos como: la propagación del calor, la propagación del sonido, la dinámica de fluidos, entre otros. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, ecuaciones diferenciales ordinarias, geometría diferencial, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

La Solución General de la Ecuación

En esta ocasión, mostraremos como determinar la solución general de la ecuación, es decir, determinaremos la colección o la familia de todas las funciones que son solución de la ecuación diferencial parcial siguiente:

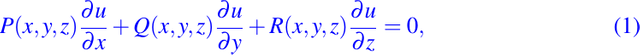
en algún dominio, que es un subconjunto del espacio euclidiano, también suponemos que las funciones P(x,y,z), Q(x,y,z), y R(x,y,z) son de clase C¹ sobre el mismo subconjunto y que ellas no se anulan simultáneamente en algún punto del dominio.

Con el fin de formalizar lo que anteriormente hemos dicho, enunciemos los dos teoremas siguientes:

El teorema anterior, lo que establece es una relación entre dos funciones que son solución de la ecuación dada por (1) y cualquier composición con una función que por lo menos sea continuamente diferenciable una vez, que también sería solución de la misma ecuación dada en (1).

En resumen los dos teroemas anteriores lo que nos tratan de decir, es que la solución general de la ecuación dada en (1) se puede siempre expresar de la forma siguiente:

donde u y v son dos soluciones fijas de la ecuación general mostrada en (1), las cuales son funcionalmente independientes y la función F es una función de clase C¹ arbitraria de dos variables.

---

---

Ejemplo

Consideremos la Ecuación Diferencial Parcial siguiente:

sobre el subconjunto de R³ que satisface que x>0.

Sobre este dominio, las funciones u y v dadas a continuación

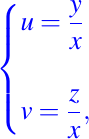
son soluciones funcionalmente independientes de ecuación diferencial parcial dada. Entonces la solución general de la ecuación es


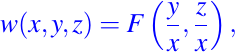
donde F es cualquier función de clase C¹ de dos variables.

---

---

Ecuaciones Cuasi-lineales

Sea la ecuación diferencial parcial cuasi-lineal dada por:

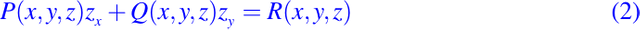
donde las funciones P(x,y,z), Q(x,y,z) y R(x,y,z) son funciones de clase C¹ sobre su dominio, a saber


las cuales no se anulan de manera simultanea para todo punto sobre este dominio.

Ahora bien, una solución dada por:

de la ecuación mostrada en (2), la cual puede considerarse como una superficie en R³ y por ende recibe el nombre de Superficie Solución de (2). Notemos que el vector normal a esa superficie es


la cual es ortogonal al campo vectorial dado por

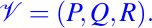
Si consideramos la siguiente función dada por:

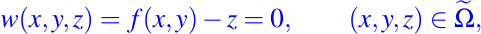
decimos que w(x,y,z) es una solución de la Ecuación Diferencial Parcial siguiente:


luego, podemos notar que:


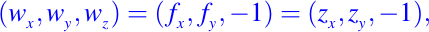
entonces tenemos lo que sigue:

---

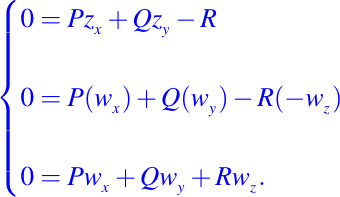
Ahora enunciemos el siguiente lema, con el cual podremos obtener la solución de la Ecuación Cuasi-lineal, también mostraremos una demostración del mismo a continuación.

Demostración:

Usando el teorema de la función implícita, tenemos:

así, diferenciando con respecto a x obtenemos


luego, diferenciando con respecto a y tenemos:


por lo tanto, nos queda que:

---

El teorema anterior nos da las herramientas para construir la solución de la Ecuación Diferencial Parcial Cuasi-lineal.

---

Ahora definiremos lo que llamaremos una Integral General de la manera siguiente:

En la práctica, las funciones u y v usadas en la Integral General F(u,v)=0, se obtienen resolviendo el sistema de ecuaciones asociado

---

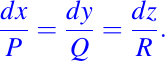
Ejemplo 1:

Encontremos la integral general de la siguiente ecuación diferencial parcial cuasi-lineal

así, el sistema asociado de ecuaciones esta dado por


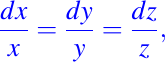
luego, si tomamos la primera igualdad del sistema anterior y resolvemos obtenemos lo siguiente:


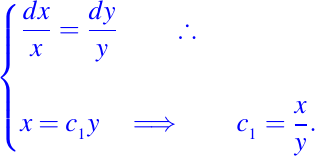
Ahora, tomando la segunda igualdad y la resolvemos tenemos:


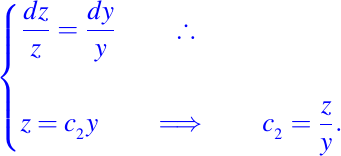
y podemos escoger


las cuales son dos soluciones funcionalmente independientes de la ecuación diferencial parcial dada por:

Por lo tanto, la integral general de

esta dada por la función siguiente:


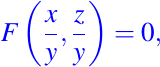
donde F es una función de clase C¹ sobre el plano R², la cual es arbitraria de dos variables. Si definimos a la función F como sigue:


de esta manera obtenemos,


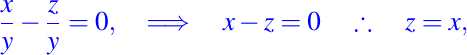
la cual es una solución de la ecuación

Si ahora definimos a la función F de la forma siguiente tenemos:

entonces obtenemos,


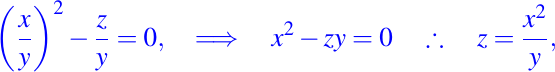
la cual es una solución de


definida en uno de los siguientes dominios y>0 ó y<0.

---

---

Ejemplo 2:

Encontremos la integral general y una solución de la ecuación diferencial parcial cuasi-lineal dada por:

Sea el sistema asociado dado por

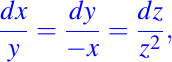
donde este es el problema equivalente para


y que podemos esribir como


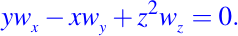
Si tomamos la primera igualdad del sistema asociado y lo resolvemos, obtenemos lo siguiente:


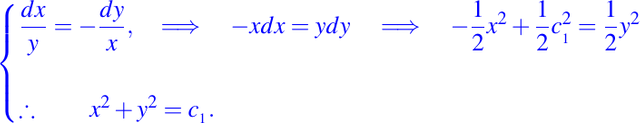
Procediendo de manera analoga para la segunda igualdad del sistema asociado tenemos


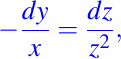
ya que


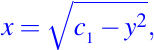
entonces


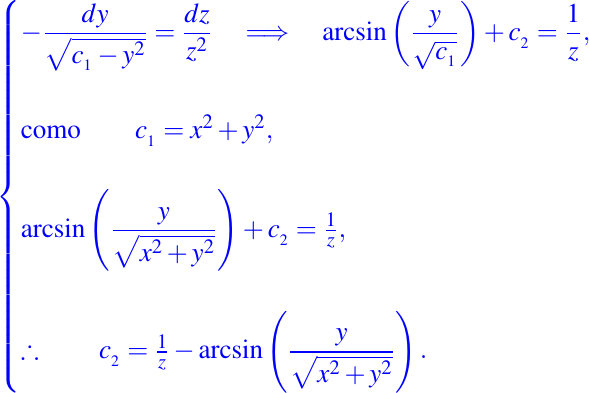
Entonces, la integral general que estamos buscando esta dada por la siguiente ecuación


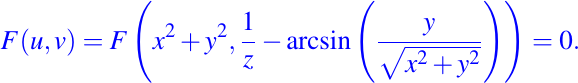
Una solución general sería por ejemplo:


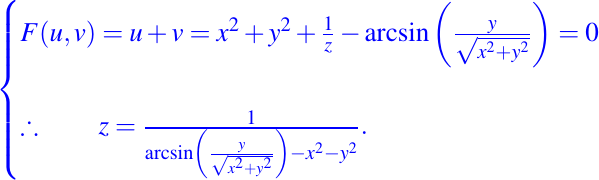
sería una solución, esta es válida para

---

---

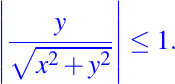
Queridos amigos y lectores, espero hayan disfrutado y aprendido en esta 4^ta Lección de la serie de Introducción a las Ecuaciones Diferenciales Parciales, de igual manera los invito para la 5^ta Lección de esta serie, donde continuaremos tratando este tema tan interesante y de mucha aplicación. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Lang, Serge. Calculus of Several Variables. Springer Science & Business Media, 2012.
• Edwards, Charles Henry. Advanced Calculus of Several Variables. Courier Corporation, 2012.
• Dennemeyer, Rene. Introduction to Partial Differential Equations and Boundary Value Problems. 1968.
• Pinchover, Yehuda, and Jacob Rubinstein. An Introduction to Partial Differential Equations. Cambridge University Press, 2005.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales Parciales, que estoy seguro serán de su interés:

Introducción a las Ecuaciones Diferenciales Parciales - Lección #1	Introducción a las Ecuaciones Diferenciales Parciales - Lección #2
Introducción a las Ecuaciones Diferenciales Parciales - Lección #3

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por abdulmath usando software libre, , GIMP e Inskcape.

---

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}