Lets discuss sequence, convergent sequence, divergent sequence and problems on them....
Sequence ,convergent sequence and divergent sequence

Sequence
In simple words, sequence is enumerated collection of objects in which repetitions are allowed.
In field of real analysis , a sequence is defined as :-
If N is a set of natural number and X be any set,then a function f: N→X is called a sequence.
If X=R or subset of R (where R is set of real number), then f is called a real sequence and if X=C or subset of C (where C is a set of complex number) then f is called a complex sequence.
A sequence generally denoted by { }, by putting values in { }.
Examples of sequence:-
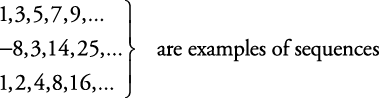
Convergent Sequence
Convergent is an important property of sequence.A sequence is converge to a particular value known as limit of the sequence.
In field of real analysis, the convergent sequence is defined as:-
A sequence is said to converge to limit l , if given ε>0 , however small, there exists a positive integer m (depending upon ε) such that:-
|an -l |<ε for all n≥m
Problem on Convergent Sequence
Problem:-1) Show that the sequence {n+1/n} converges to 1.
Solution:- Let {an}={n+1/n}
Now consider given ε>0, however small, we choose a natural number m such that:-
m>1/ε or 1/m <1/ε
Therefore, for all n≥m or 1/n ≤1/m we have:-
|an -1| = |n+1-n/n| = 1/n but 1/n≤1/m <ε
Therefore, |an -1|<ε for all n≥m
⇒ limit n→∞an =1
Hence sequence {n+1/n} converges to limit 1.
Divergent Sequence
A sequence is said to be divergent, if it is not convergent.This means a divergent sequence doesn't converge to a finite value of limit. The value of limit of divergent sequence is infinite (+∞ to -∞)
In field of real analysis:-
- A sequence {an} is said diverge to +∞ if k>0 however large, there exists a positive integer m(depending upon k) such that :-
a n > k for all n ≥ m
- A sequence {an} is said diverge to -∞ if given k>0, however large, there exists a positive integer m(depending upon k) such that :-
a n <-k for all n ≥ m
Problem on divergent sequence
Problem:-2) Show that the sequence {n2 + 3n} diverges to +∞ .
Solution:- Let given sequence is {an} where an = n2 + 3n
Let k>0 however large--
Now an > k
if n2 + 3n > k
if n2 > k-3n
if n > √k - 3n
Now let a positive integer m just greater than √k - 3n
⇒ an > k for all n≥m
Therefore {n2 + 3n} diverges to +∞ .
Citations:-
(https://pixabay.com/en/geometry-mathematics-volume-surface-1044090/)(only background of image 1)..
(https://en.wikipedia.org/wiki/Sequence) ( only simple definition of sequence is used)..
(https://www.cliffsnotes.com/study-guides/algebra/algebra-ii/sequences-and-series/definition-and-examples-of-sequences) ( only first image of site is used as in example of sequence)
(https://en.wikipedia.org/wiki/Limit_of_a_sequence) ( simple definitions for convergent and divergent sequences are modified from here)..
Congratulations, your post had been chosen by curators of eSteem Encouragement program. Feel free to join and reach us via Discord channel if you have any questions or would like to contribute.
Also,
CREATING YOUR PROFILE IS EASY! JUST FOLLOW THE STEPS HERE ☜(ˆ▿ˆc)
You can trade your earned credstars for SBD!
Thanks.
Congratulations @amansharma555! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
SteemitBoard and the Veterans on Steemit - The First Community Badge.