Diffusion in Porous Media – A world of applications – Part 3
Hello, dear friends of Steemit! Again with you, this time with the third post about diffusion in porous media.
In the two previous posts, I mentioned that I have a degree in Physics and currently I work as a professor in the Faculty of Sciences of the University of Zulia in Venezuela, and besides I work in the investigation of transport phenomena such as the diffusion of matter and thermal conduction in porous media.
I also mentioned that there are two approaches to study the notion and the phenomenon of diffusion: the phenomenological approach using the so-called diffusion laws of Fick and their mathematical consequences, and the approach statistical physicist, which considers the random path of the diffusing particles propelled by its thermal energy.

In the second post, I talked about the diffusion process through the phenomenological approach, their types and the Fick equations of diffusion.
In this third post, I will talk about the diffusion process following the statistical physical approach, or atomistic, as it is also known, that considers the random walk of the diffusing particles.
From the atomistic point of view, the diffusion is considered as a result of the random walk of the diffusing particles. The random walk of small particles in suspension in a fluid was discovered in 1827 by the scottish botanist Robert Brown. In his honor, this transport phenomenon takes his name.

So, the diffusion can be considered a macroscopic manifestation of Brownian motion on the microscopic level. Thus, it is possible to study diffusion by simulating the motion of a Brownian particle and computing its average behavior. A few examples of the countless diffusion processes that are studied in terms of Brownian motion include the diffusion of pollutants through the atmosphere, the diffusion of electrons through a semiconductor, and the diffusion of minerals through bone tissue in living organisms.
The theory of the Brownian motion and the atomistic backgrounds of diffusion were developed by the german physicist Albert Einstein and the polish physicist Marian Smoluchowski.
A BIT OF HISTORY ABOUT THE BROWNIAN MOTION
The irregular movement of microscopic particles suspended in a liquid had been warned long before the botanist Robert Brown, in 1827, observed through the microscope microparticles that had a random movement when they were suspended in a medium. Doing a systematic job, Brown ruled out that Brownian motion occurs for any biological cause. This phenomenon lacked explanation until the kinetic theory of matter was developed.
In 1858, the french Jules Regnault suggested that this behavior is due to the absorption of light giving rise to microscopic movements of currents. In 1879, the scottish chemist William Ramsay proposed a molecular explanation of the Brownian movement, assuming the existence of collective movements of large numbers of atoms of liquid. The fact that the Brownian motion must constitute a physical phenomenon in itself, where the molecules of the fluid medium collide with the microparticles, was proposed in 1880 by the french Jean Delsaux.
In the search for an argument that proved the existence of molecules, Albert Einstein, in 1905 explained that such behavior is due to the multiple collisions of the particle with the molecules of the medium. Derived an equation for the macroscopic diffusion coefficient, and proposed an experiment to measure the mean square displacement of the Brownian particle. Following a different model in 1906, Smoluchowski proposed a kinetic-molecular explanation of brownian motion, assuming that deviations from trajectories were produced by virtual particles that represented a cluster of fluid molecules, also using the mean free path theory of gases.

The french physicist Paul Langevin, in 1908, proposed a version of Newton's equation of motion for a brownian particle in a fluid and arrived at the same result for Einstein's mean squared displacement.

That same year, inspired by the work of Einstein, the french physicist-chemist Jean Perrin made experimental observations of the trajectories of many suspended particles of different sizes and calculated the number of Avogadro. This work finally removed all doubts about the validity of the kinetic theory of matter, for which Perrin received the Nobel Prize in Physics in 1926.
WHAT IS THE BROWNIAN MOTION?
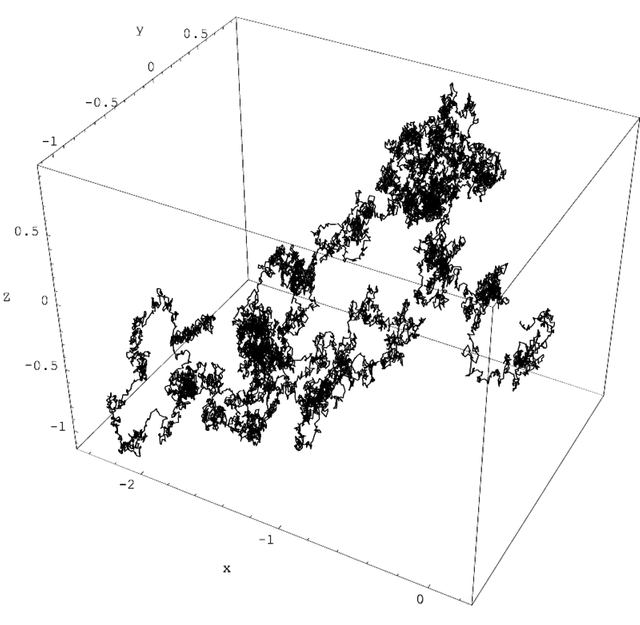
The brownian motion or brownian movement, as it is also known, is the incessant and irregular or random motion of particles of sizes between 10-9 m and 10-6 m suspended in a fluid as a resulted from their collision with the atoms or molecules in movement of the liquid or gas.

In 1827, Robert Brown, while looking through a microscope at particles trapped in cavities inside pollen grains of Clarkia Pulchella, then a newly discovered species of flowering plant, in water, he noted that the particles moved through the water with a “rapid oscillatory motion”.
Other researchers had noticed this phenomenon earlier, but Brown was the first to study it. Initially he believed that such motion was a vital activity peculiar to the male sex cells of plants, but he then checked to see if the pollen of plants dead for over a century showed the same movement. Further study revealed that the same motion could be observed not only with particles of other organic substances but even with chips of glass or granite and particles of smoke.
The atoms and molecules had long been theorized as the constituents of matter, and Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.
PROPERTIES OF THE BROWNIAN MOTION
The Brownian movement has the following properties:
- The speed of movement is greater when the size of the suspended particles is smaller.
- The Brownian particle velocity is not an easily measurable quantity, since the particle trajectory it is not a differentiable quantity due to abrupt changes in direction.
- It is very stable over time.
- It depends on the nature of the fluid.
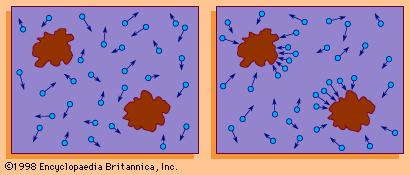
The mechanisms responsible for this behavior are the molecular collisions. In this way it can be assumed that the irregular movements of the particles are the product of the transfer of energy and momentum of the molecules of the fluid to the particle through the collisions.
THE EINSTEIN'S THEORY OF THE BROWNIAN MOTION
The model proposed by Einstein is based on two fundamental assumptions: (1) the brownian particle motion is caused by many collisions from the surrounding medium molecules, and (2) can be described probabilistically in terms of statistically independent collisions and very frequent.
The Einstein's argument was to determine how far a Brownian particle travels in a given time interval. The Classical Mechanics is unable to determine this distance because of the enormous number of bombardments a Brownian particle undergo, roughly of the order of 10-14 collisions per second. Einstein taked into account the collective motion of Brownian particles.
Einstein derived a partial differential equation of the probability density for a particle that is in the position x in time t, which has the same form as the second Fick's equation of diffusion:
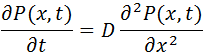
where:
represents the probability density for a particle that is in the position x in time t.
is the diffusion coefficient or diffusivity of the substance in the medium.
The equation proposed by Einstein has a solution of the form:
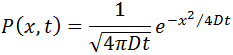
From this equation the mean squared displacement of a Brownian particle is calculated, being this:
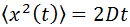
where:
I hope you enjoyed the publication about the research in which I work and that the information is your useful, I will gladly clarify your doubts and concerns about the subject. Thanks for your kind reading.
I wait for you in the fourth installment, where I will talk about some of the specific results obtained from studies on diffusion in porous media.
If you are interested, I leave the link of the previous article of the series:
Diffusion in Porous Media – A world of applications – Part 1
Diffusion in Porous Media – A world of applications – Part 2
Electronic sources:
Fuentes impresas:
Bird, R. B., Stewart, W. E. y Lightfoot, E. N., 1996. Fenómenos de transporte, Reverté S.A., México D.C., México, pp. 16-3, 22-1.
Brown, R., 1827. On the particles contained in the pollen of plants and on the general existence of active molecules in organic and inorganic bodies. Philosophical Magazine, 1, 464-486.
Einstein, A., 1905. On the movement of small particles suspended in stationary liquids required by the molecular-kinetic theory of heat. Annales the Physics, 17, 549-560.
Reif, F., 1965. Fundamentos de física estadística y térmica, vol. 1. Mc-Graw Hill.
Mazo, R. M., 2002. Brownian Motion. Fluctuations, Dynamics and Applications, vol. 1. Oxford University Press Inc.
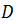
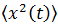
Saludos mi estimado. Excelente post y trabajo de investigación.
Gracias hermano @moroso. ¡Saludos y un abrazo!
Congratulations @hugobohor, this post is the second most rewarded post (based on pending payouts) in the last 12 hours written by a User account holder (accounts that hold between 0.1 and 1.0 Mega Vests). The total number of posts by User account holders during this period was 3384 and the total pending payments to posts in this category was $2221.32. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.
Thank you @bitgeek!