How likely for two people in a room to have the same birthday? (or The Birthday Paradox )
Today we have another cool paradox to share with you! and just to make sure it is fun enough, it has to do with birthdays!
And no, the post has nothing to do with my birthday, it's not even my birthday, but if you want to send me a gift, I definitely won't mind the gesture ! :)
Orrr if you know someone who's bday is today, you might want to send them this post, as a gift lol
Anyhowwww, what is it with the birthday paradox? let's dig in..

The birthday paradox
The paradox relates to answering the question of
How likely is it, in a room with random people, to find two having the same birthday?
So basically it drills down to figuring out the number of people in a room needed to make this a possibility.
It clearly has to be more than one person.
Two is our starting point, yet clearly it would have a very unlikely probability, at least for random people, which is a given in the statement of the problem.
Where does it start getting a good probability, say a 50% probability of finding two random people in the same room with the same birthday?
The 50% possibility
So what numbers do you have in mind? would 50 people be enough so that we have 50% of finding two with the same birthday? considering that we have 366 days in a (leap) year, 50 accounts for less than 15% of the total number of days. Maybe 100? or even half of the number of days, say 183 (366 / 2) ?
Actually, NO. None of those is the answer.
The answer is that actually we would only need 23 people in a room to get a 50% possibility for at least two people having the same birthday.
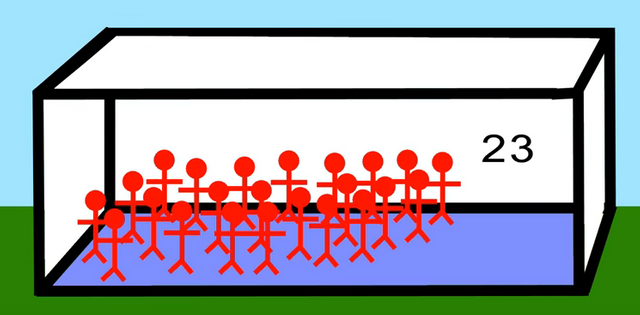
I can tell this sounds pretty counter-intuitive. But wait, before running to the explanation, the other mind-boggling answer is that if we get 70 people into a room, there is a 99.9% possibility of two having the same birthday. Yes Seventy .. 70.
The 100% probability of course remains at the total number of days of the year, +1, so at 367 people in a single room.
The full picture
Check out below graph and tabular chart for a complete perspective about the probability in relation to number of people in the room. You can clearly see the 23 at 50%, 50 people would get 97%, and 70 would be at 99.9%
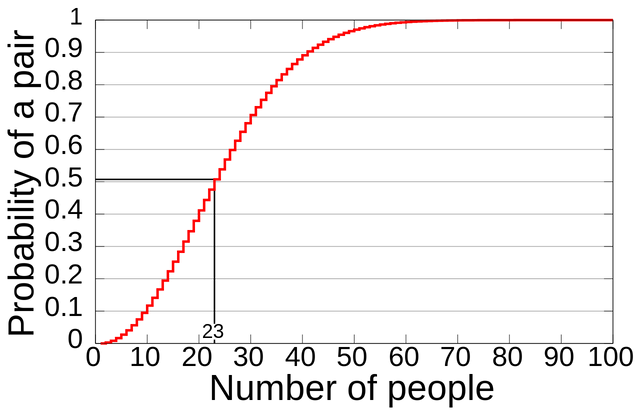
Graphical view for the probability based on number of people
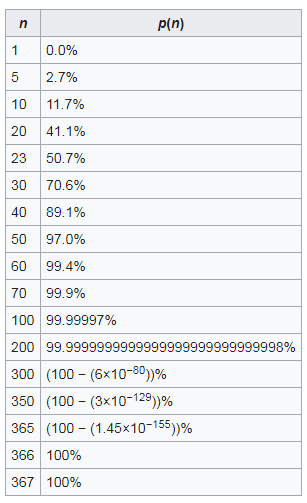
Tabular view for the probability based on number of people
What gives?? well, let us head to the proof..
The proof !
It all really drills down to probability. Since we are studying how likely it is to find two people with same birthday in a room, we need to rely on probability for the calculations.
To simplify the problem, we will make some assumptions which have little effect on the outcome, and define our steps forward:
- we will use 365 day years instead of 366 days
- we will assume every day of the year is equally likely to be birthdays.
We will also actually calculate the opposite case of our sought probability (let's call this P(A)), meaning the probability of no two people having the same birthday (call that P(A')), and decrement that outcome out of 1, bringing us the probability of two people being in the same room.
Essentially P(A) = 1 - P(A').
So, as it is clearly established, when we have a single person in the room, the problem is not valid.
When we have two people in the room, the second person's birthday, to be different than the first person, would have a probability of P(A) = 364/365 (skipping the single day of that first person).
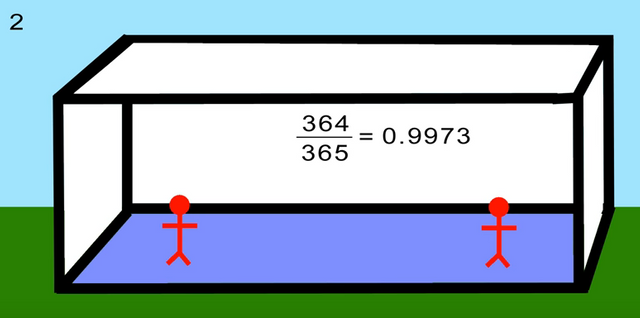
In a similar manner, when we add a third person, this person would need to avoid both birthdays of person A and B, and hence his probability would be a multiplication of the prior product, and hence P(A) = 364/365 * 363/365 (skipping 2 days this time)
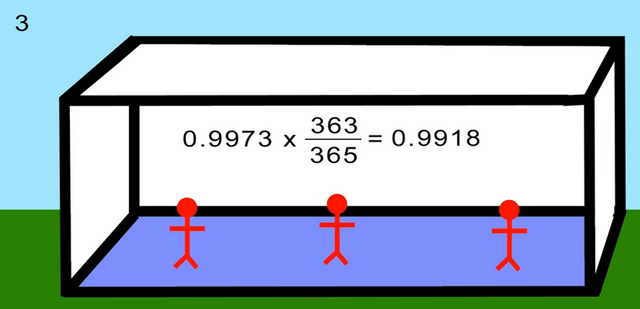
As we keep adding individuals, and reach the 23rd person, the equation is adding up, and the probability P(A') = 364/365 * 363/365 * ... * 343/365 ≈ 0.4927 ≈ 49.27%
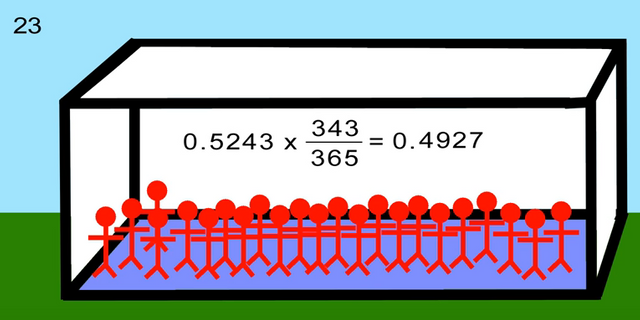
Now, to calculate P(A), we would need to use 1-P(A') ≈ 1-0.4927 ≈ 0.5073
which leads us to our previously claimed answer of 50.73%
In a similar manner, the additional probabilities can be calculated utilizing the same approach, with the generalized formula going as follows:
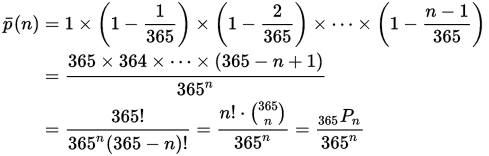
p(n) here references the opposite probability of two people not having same birthday.
Some history about the paradox
While the original history of the paradox remains unconfirmed, yet different references point to either Harold Davenport, the English mathematician, whose actual involvement is not clear nor well documented, but also to Richard von Mises, a German scientist and mathematician whose proposal was one of the earliest tracked to the birthday paradox, and to Martin Gardner, American popular mathematics and science writer, whose work on the paradox was featured in a 1957 column on the Scientific American magazine.
Thank you for reading through, and I hope you enjoyed it!
And if you're the 23rd reader, there is a 50% possibility that it is your bday, so happy birthday :)
In case this is the first paradox you see written by me, you missed some awesome brain teasers!. Make sure to check out some of my recent ones:
- Do All Numbers Converge? The Collatz Conjecture And A Wordpress Plugin Simulator
- How Many Balls Are In The Vase At Noon? (or The Ross-Littlewood Paradox)
- Hilbert's Grand Hotel Paradox
- The Napkin Ring Paradox
References:
Photo Credits:
Founder of Arab Steem
Arab Steem is a community project to expand Steemit to the Arab world, by supporting the existing Arab steemians and promoting others to join.
You can connect with us on @arabsteem or via discord channel https://discord.gg/g98z2Ya
Your support is well appreciated!
Proud Member Of
- steemSTEM: SteemSTEM is a project that aims to increase both the quality as well as visibility of Science, Technology, Engineering and Mathematics (and Health). You can check out some great scientific articles via visiting the project tag #steemSTEM , project page @steemstem, or connecting with us on chat https://steemit.chat/channel/steemSTEM
- MAP(Minnows Accelerator Project): MAP is a growing community helping talented minnows accelerate their growth on Steemit.
To join, check out the link at the home page of @accelerator account
The birthday 🍰 paradox is by far my favorite! How did you know I love Birthdays!
hahaha, celebrating a full month of bday kinda gives me a hint :P
its my also favourite @kubby
frankly telling math is over my head LOL
haha, hope you enjoyed it at least
well done dear brother.
Thank you Khaled :)
Thanks for attending Pimp Your Post Thursday @mcfarhat. I have written a post to share your featured post. Just stopping back to let you know that you can see your name in lights right here. (Just kidding about the lights :)
lights or no lights, thank you ! :)
Another amazing (and fun!) post by @mcfarhat!
Without knowing, I guessed just over 20... LOL! That's based on our weird little town. I know most everyone's birthday and I feel like on ANY given night if the bar had more than 20 people, there were at LEAST two with the same birthday.
I'm a stranger case still, sharing a birthday with (at least) 4 others in town, two being a father/son.
Maybe our town is a perfect sample of all things. A microcosm, if you will.
thank you !!
haha well done! i wouldn't have guessed it myself TBH :P
your microcosm is fascinating indeed hahaha
What if you are born on the 29th February... xD
hahaha I told you you're too smart for your own good! now go grab that cup of coffee :P
hot choc... lol :P
hahah but of course !!
thanks for the information provided this something interesting :)
Thank you
I do like probability stuffs!
Thank you, glad to hear :)
I do find them simply amazing !
I didn't know this was a paradox. Looks so logical :D
hahaha exactly :P
counter intuative but pretty straight forward indeed. Must say, needed your explaination before ot struck me. The interesting thing with statistics is that it can give results that we would not expect. That is why statistics is a wonderful way of looking at things.
yes thank you, which is why it's a paradox :)