Instability In Chaotic Systems: Predicting the Future From Present in a Deterministic Chaotic System
Hi, and welcome to my blog. Today I will continue my discussion on chaotic systems. Recently two things have become very chaotic around me. The first one is the weather in my area. It has become so erratic that you cannot even say for sure what is going to happen in the next 30 minutes. It particularly affected me because my solar system has not been given me the estimated power output for weeks now. In a moment the sky would appear clear, and I can “feel” the sunlight being trapped by my PV panels, but just before I could finish rejoicing, it becomes cloudy again. If we go back to the history of chaos, you will recall that the word came out from the observation and study of weather, so it is not special that I have a chaotic weather condition.
The second thing, perhaps peculiar to just me is the ongoing world cup predictions I made. It has become evident that the games are sensitive to changes in initial conditions. I supported African teams and a few European teams too. Don’t blame me, African due to my origin and some specific European teams for my love for good football. The outcome has become so erratic that even the games that you think will end in a tie are being turned around by “die” minute goals! Just a little mistake, omission or fouls committed can turn the games around. You will agree it is not new in football to experience such an upset.
Chaos is just everywhere. You will observe it if you are careful enough even though you are not dealing with some real physical data. I will continue to discuss chaos here, maybe for a few more posts before my research results start coming out. You will observe in my title above I have mention two terms. Vis: “predictability and deterministic” which seem a bit conflicting right? Well let me explain, and I am sure by the end of this post you will get the information I am trying to get across.
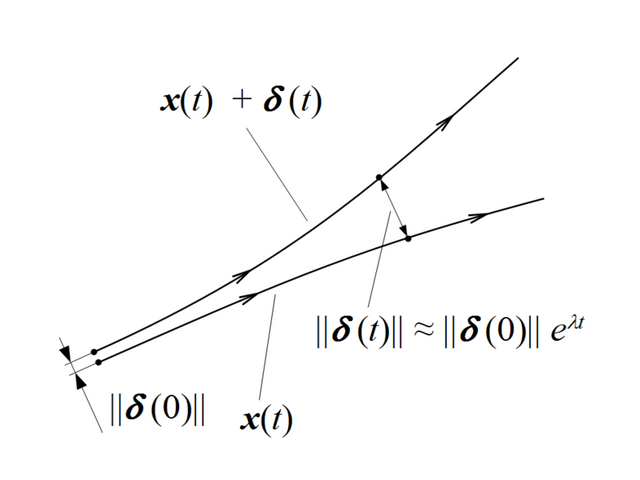
[image credits: Wikimedia commons under the Creative Commons CC0 1.0 Universal Public Domain Dedication] 𝛌 in the equation written on the right bottom corner is the Lyapunov exponent.
In my last post on the subject matter, I tried to distinguish between the different types of nonlinear dynamical system. I used the Lyapunov exponent as a major characterization of chaotic motion. It is important to state here that there are many methods that can be used to characterize nonlinear deterministic system, but I have chosen the Lyapunov exponent in my research work for a number of reasons.
I will zoom in now on chaos and also explain the reason for using Lyapunov exponent for characterization of nonlinear systems.
[image credits: Wikimedia commons under the Creative Commons Attribution Share Alike 4.0 International license]
Generally you will believe that similar causes should have similar effect as some everyday occurrences suggest right? However this is not valid for chaotic system on a long term scale. In essence, what I am saying is that determinism of a chaotic system is, but for a short period of time. We might be tempted to think that this is as a result of external influence on the system, but if such is the case then we should not be talking about chaos. However, chaotic systems are inherently chaotic. You might want to remember that.
The unpredictability in chaotic system is a direct consequence of the intrinsic instability of the system caused by its high sensitivity on initial conditions. Small changes that can be trivial in other systems can cause a major difference in the outcome of a chaotic system.
When the instability nature of a chaotic system is investigated, a number of concepts may emerge. Two possible but yet related concept that will emerge are Kolmogorov-Sinai entropy while the second is a simple geometry in which nearby trajectories separate exponentially and at a fast rate over time. This is the concept of Lyapunov exponent which deals with the exponential divergence of trajectories in a chaotic system.
By the way, let me narrow down a bit more on what I mean by exponential divergence. Divergence obviously mean deviation or separation, so in actual sense, what I mean is that the trajectory of two close initial conditions becomes more separated as a function of time.

[image: Visual representation of a Strange attractor credits: Wikimedia commons under the Creative Commons Attribution-Share Alike 3.0 Unported license]
Well, it wouldn’t be if it happens slowly and one can see a pattern as predominantly experienced in periodic systems. For chaotic systems, the divergence is exponentially fast!
The properly averaged exponent of this increase in separation between close trajectories is characterized by the Lyapunov exponent, which quantifies the strength of chaos.
The number of Lyapunov exponents that can be defined for a system is a function of the phase space dimension. That is, a system can have more than one Lyapunov exponents.
The one of particular interest which I will be discussing more on is the Maximal Lyapunov Exponent
If the Maximal Lyapunov Exponent (𝛌) of a system is positive, and there is an exponential divergence of close trajectories which is an indication that the system is chaotic.
It is important to state here that the two nearby trajectories cannot be farther apart than the size of attractor
It is not uncommon for the Maximal Lyapunov exponent in a dissipative system to be negative. This is an indication of a stable fixed point which is not regarded as a chaotic system. Two trajectories which approach the attractor of the fixed point also move closer to each other exponentially fast.
If the system motion settles down to a limit circle, then the two trajectories considered will only come close or separate slower than exponentially.
Let’s now have a summary table for the type of motion I have described above and their corresponding Maximal Lyapunov exponent:
- In a stable fixed point, the maximal Lyapunov exponent 𝛌 < 0
- In a stable limit circle, the maximal Lyapunov exponent 𝛌 = 0
- In a chaotic system, the maximal Lyapunov exponent 0 < 𝛌 < ∞
- Noise, the maximal Lyapunov exponent 𝛌 = ∞
I mention noise because it is worth explaining in the concept of Lyapunov exponent. It occurs when a deterministic system is predominantly perturbed by random noise. In fact, on a small scale, the noise system can be characterized by diffusion process, thus making the maximal Lyapunov exponent infinite. This is in accordance to mathematical definition [[1]].
When computing the numerical values of the Maximal Lyapunov exponent, proper normalization must be taken into account. When the data under consideration are turned into map-like data by methods such as the Poincaré surface of section, it is important to know the average time between any two subsequent points of the Poincaré map.

[image credits: Pixabay:CC0 Creative Commons]
Like I mentioned earlier, there are various ways of quantifying the properties of a signal, and a few turned a data set into a number.
One interesting thing about the Lyapunov exponent is that it remains invariant under any form of transformation provided that the transformation is smooth. What that means is that the Lyapunov exponent is unaffected by changes such as scaling, shifting, or otherwise process of the data which gives freedom of choice of the precise method of state space reconstruction.
In essence, what I am saying is that the Lyapunov exponent as well as methods such as correlation dimension are robust, in that they enhance our understanding of the underlying system dynamics rather than just compressing the data into a number. This is because they do not depend significantly on factors such as the coordinate used measurement procedure etc. i.e. the effect of these factors on them is trivial.
This explains the interest in using the Lyapunov number to characterize chaos as it offers the same result anywhere as long as the system under consideration is the same.
Needless to say, before my data set will be investigated for chaos, it must have a maximal Lyapunov exponent which is greater than 0.
To determine the value of the Maximal Lyapunov exponent for a given time series data, various algorithms has been developed.
One was suggested by Wolf et al in (1985), but has lost its popularity due to some of the challenges it present. First, the algorithm does not test for divergence in the trajectories but assumes its existence. Therefore, it can give a finite exponent for stochastic data even though the exponent is supposed to be infinite. [[1]]
Other useful algorithms include the ones proposed by Sano and Sawada (1985), Eckmann et al, (1986) which are very efficient.
However, for the data set I will be working on, I will be using the algorithm introduced recently by Rosenstein et al, (1993) and Kanz (1994) independently. The advantage this algorithm has is that it tests directly for divergence before computing the Lyapunov exponent.[[1]] The allow us to see the true nature of the time series data before even going into proper investigation, but not assuming the data to be chaotic.
Summary
Predictability of deterministic chaos is desirable but the sensitiveness of the system to initial conditions makes it difficult over a long period of time. Chaos theory still remains a fast growing field of study in contemporary science with a lot yet to be reconciled and agreed upon. Knowledge of instability and chaotic behavior in system would help to improve our models of real life events and further close the window between theory and real life applications.
References
Holger Kanz and Thomas Schreiber:Nonlinear Time Series Analysis.Second Edition. Cambridge University Press. ISBN 0-521-52902-6
CHAOS: Introduction to Dynamical systems. Kathleen T. Alligood, Tim D. Sauer, James A. Yorke. Springer: ISBN 0-387-94677-2
PS: The first two materials in my reference list are the main source of information in my quest to using nonlinear dynamical tools on ionospheric TEC data I am working on.
Thank you for visiting my blog. You too can be a part of the wonderful community @steemstem.
If you write STEM related content, (Science, Technology, Engineering, and Mathematics) consider joining #steemSTEM on discord here. If you are from Nigeria, you may also include the #stemng tag in your post. You can visit this blog by @stemng for more details.

Impressed with your ability to speak the language of math and yet present it in a way in which I can enjoy what you're saying despite lacking a large mathematical aptitude.
So interesting to consider chaos and as I was reading, and applying mentally, mainly to relationships--as in people.
You write, "It is important to state here that the two nearby trajectories cannot be farther apart than the size of attractor." How fascinating to think about how that space (chaotic firings, but still lines within a circle) can become much bigger providing that common point has more pull.
There is such a beauty in the macro view of it all! Thank you for giving me something compelling to think abut today :)
I'm glad it was useful. I try to keep it simple for all to understand.
Chaos theory is robust and is finding application inmany spheres of life.
Chaos is also finding application in psychology.
Thank you for your encouraging comment
A positive Lyapunov exponent does not always yield a choatic system. For example, consider the map which maps x to 2x where x is in R. The lyaponov exponen is positive but the map is clearly not chaotic.
Thank you for your usual perusal @mathowl.
Before the positive Lyapunov exponent will be tested, the exponential divergence must have been checked, which is a first requirement before computing the Lyapunov exponent. Also, I am using other methods such as the correlation dimension.
The TISEAN software I am using is that developed by Holger Kanz so it is just necessary I discuss what he has to say on the subject matter as referenced in[[1]]
You will agree with me that there are lots of arguments still going on about the best way to characterized chaos. That was why I clearly stated that I am writing in the confines of the methods and tools I am using. (See my last statement before the thank you message)
Any suggestions on the best way to characterize will be appreciated.
So let's take an ODE x'=2x with x in R^2. Could you show that the maximal Lypunov exponent is positive and explain why this system is not chaotic?
Note that if the maximal Lyapunov exponent is positive (and exists in the sense that the limit converges) then there is exponential divergence
I tried to avoid mathematical expressions (I leave that for the mathematicians). Let try to give an equation here.
Consider Xn1 and Xn2 as two points in phase space with distance ||Xn1 – Xn2|| = δ0 << 1
Let δΔn be the distance between the trajectories of these two points some later time Δn
Then:
δΔn = || Xn1 +Δn - Xn2+ Δn||.
The Lyapunov exponent 𝛌 is determined by:
δΔn ≈ δ0e𝛌Δn,
With δΔn << 1 and Δn>> 1
This equation remains valid provided that the limit converges like you have rightly said and then there will be exponential divergence if 𝛌 is positive.
Other methods such has phase space method, false nearest neighbors; correlation dimension etc. will also be used on the data set I am working on.
It is however not all close trajectories that will eventually have this (that is the essence of false nearest neighbor) and so the consideration is only on those that fulfill this requirement.
I think the challenge here is that I am working with real data, i.e. (actual scalar measurement as most physics research using nonlinear dynamical tool), so in a way, we have to use a proper embedding dimension that fits the data. Then we also consider modeling the physical system.
Perhaps when I finish collecting my data and start my analysis, it would be much more clearer the angle from which the TISEAN software will be computing and searching for chaos in the data set.
Thank you and I look forward to our discussion on the chaos this week. I really want to have a robust research and I can use any help I can get.
Edit: to add, I agree that the estimated finite dimension and Lyapunov exponents on their own cannot be a suitable prove for strict nonlinear determinism if a clear scaling region cannot be established. One suggested way to avoid this is to test first if the data could be explained by a linear model. Some literature suggested the use of surrogate data
Hey @obamike
Here's a tip for your valuable feedback! @Utopian-io loves and incentivises informative comments.
Contributing on Utopian
Learn how to contribute on our website.
Want to chat? Join us on Discord https://discord.gg/h52nFrV.
Vote for Utopian Witness!
You didn't answer my question.
Somehow I missed this. You want me to prove the math model you wrote in your comment right?
Well, perhaps I can do that in a post when I am much stable.
Well done....
Thank you for visiting my blog
Always man... Keep it coming
Hi @obamike!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV