Optimización Matemática en Modelos de Programación Lineal aplicados a la vida cotidiana, Método Simplex de las dos fases
La optimización matemática tiene una gran variedad de aplicaciones tanto en la industria como en los negocios, dentro de esta área del conocimiento la Programación Lineal ha tenido una gran relevancia en el siglo XX debido en parte a su utilidad en la planificación empresarial, en el transporte y asignación de recursos. Uno de los métodos más conocidos para tratar este tipo de problemas es el Método Simplex, el cual es el objeto de estudio de este artículo.
En un artículo anterior se modeló un problema típico de optimización mediante el método Simplex, en el presente artículo se analizará como cambian los Modelos de Programación Lineal al añadir una restricción de tipo mayor o igual, en cuyo caso se requiere la aplicación de un nuevo método, específicamente el Método Simplex de las dos Fases.
El problema en cuestión se basa en una situación de maximización de ganancias extraída de la vida cotidiana.
Modelo Matemático extraído de una situación cotidiana
La señora Medina elabora hallacas durante todo el año en la ciudad de Coro, en diciembre del año 2017 ella dispone de Bs 5.000.000 para invertirlos en la elaboración de hallacas, el costo para elaborar el relleno de cada hallaca es el siguiente:
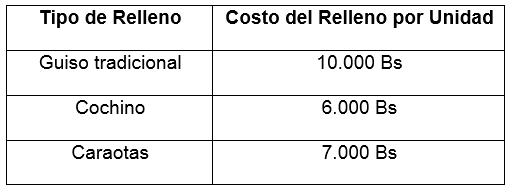
Tabla sobre el costo del relleno. Fuente: Elaboración propia
El costo de las hojas de plátano para envolverlas es de 1.000 Bs por cada hallaca, el costo de la harina y los otros ingredientes es de 8.000 Bs por hallaca, el costo del pabilo gastado para amarrar una hallaca es de 500 bs. La comunidad del sector le solicita a la señora Medina que elabore como máximo 120 hallacas que no sean de guiso tradicional, adicionalmente como medida para controlar el colesterol de la población, la comunidad le ha pedido a la señora Medina que el número de hallacas de guiso tradicional más el doble de hallacas de cochino sea a lo sumo 200, si cada hallaca se vende en 25.000 Bs. Determine los niveles de producción de hallacas que maximizan las ganancias de la señora Medina de conformidad con su presupuesto y las restricciones impuestas por la comunidad.
En el artículo anterior se demostró que para dicho problema el siguiente modelo de programación lineal permite encontrar la solución óptima:
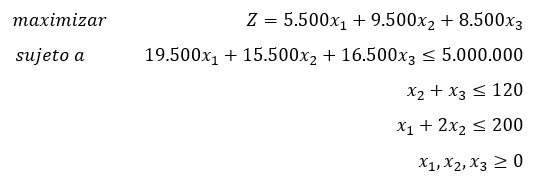
Donde x1, x2 y x3 representan el número de hallacas de guiso tradicional, cochino y caraotas respectivamente. Sin embargo, si se añade una restricción más del tipo >= al problema en cuestión, el modelo matemático cambia, por ejemplo, si la comunidad del sector le exige a la señora Medina que elabore por lo menos 30 hallacas de cochino, esta restricción se expresa de la siguiente forma
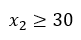
Quedando el modelo final
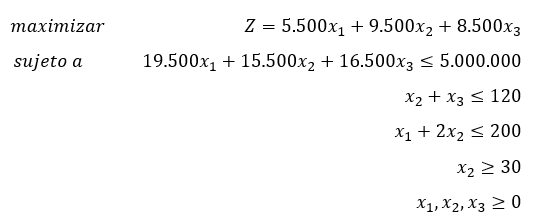
Los modelos de Programación Lineal que involucran restricciones de tipo >= o = requieren la aplicación del Método Simplex de las dos fases para obtener su solución, a continuación se detalla el funcionamiento de este método.
PRIMERA FASE
Para la primera fase del Método Simplex este modelo se expresa en forma típica al convertir cada restricción de tipo >= en una igualdad mediante restar una variable de superávit agregada y añadir una variable artificial, para la restricciones de tipo <= se añade una variable de holgura, y para la restricciones de tipo = se añade solamente una variable artificial, se denotarán las variables de holgura con (h), las de superávit con (s) y las variables artificiales con (a), en la primera fase la función objetivo se sustituye por la minimización de la sumatoria de las variables artificiales (independientemente de si el problema general se trata de maximizar o minimizar), esta sumatoria se denotará por x0, expresando el modelo de la siguiente forma:

Que se reescribe como

Dicho modelo se representa de forma tabular colocando en la base solo las variables de holgura y las variables artificiales correspondientes a cada restricción, tal como se muestra a continuación (la variable x0 no se representa en la tabla)
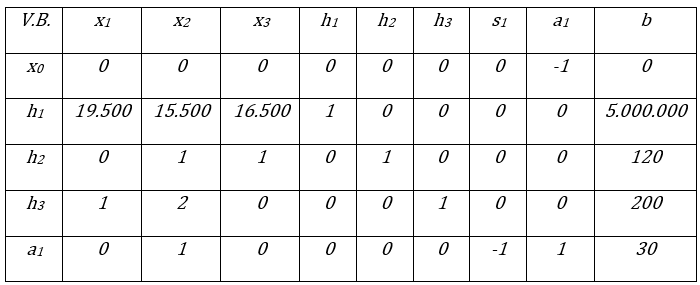
Tabla Inicial del Método Simplex de las dos Fases. Fuente: Elaboración propia
Sin embargo, los coeficientes de las variables básicas deben ser iguales a cero en la función objetivo lo cual se logra al sumar a la fila x0 La fila a1 obteniendo la siguiente tabla
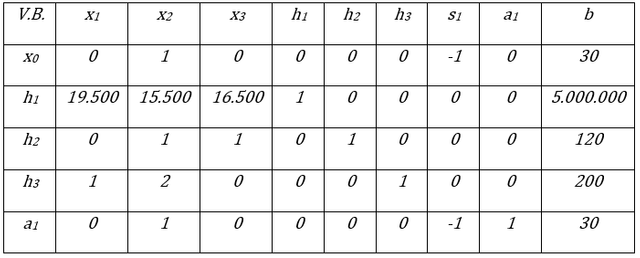
Tabla Modificada del Método Simplex de las dos Fases. Fuente: Elaboración propia
Una vez determinada esta forma tabular se procede a resolver aplicando operaciones similares a las transformaciones algebraicas de Gauss-Jordan en matrices, se debe determinar una variable entrante y una variable básica saliente en cada iteración, según Taha (2012) el criterio a usar es el siguiente:
A) La variable de entrada en un problema de maximización (minimización) es la variable no básica con el coeficiente más negativo (positivo) en la fila Z, el óptimo se alcanza en la iteración en las cual los coeficientes en la fila Z son no negativos (no positivos).
B) La variable de salida es la variable básica asociada con la relación mínima no negativa con el denominador estrictamente positivo.
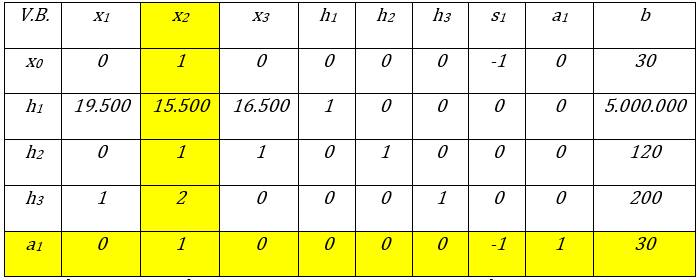
Iteración N° 0 de la primera fase del Método Simplex. Fuente: Elaboración propia
Como se trata de minimizar, los coeficientes de las variables de holgura y superávit deben ser negativos para estar en el punto óptimo. Por lo tanto aplicando los criterios del método Simplex se obtiene:
Variable Entrante (VE): x2 Por ser el valor más positivo en los coeficientes de las variables
Variable Básica Saliente (VBS): a1 Debido a que la relación 30/1=30 es la menor, 200/2=100; 120/1=120; 5.000.000/15.500=322,58 arrojan valores superiores a 30.
En la fila 5 el elemento pivote es igual a 1, por lo tanto no es necesario hacer cambios en dicha fila, para las demás filas los elementos en la columna pivote deben ser iguales a cero lo cual se logra aplicando las siguientes operaciones de fila
(F1 se usa para denotar la Fila 1 y así sucesivamente)
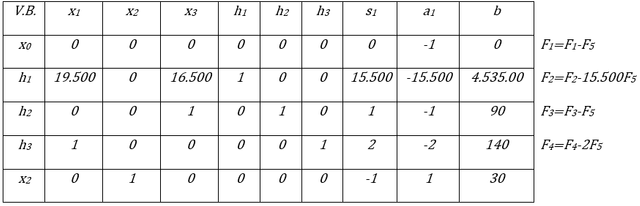
Iteración N° 1 de la primera fase del Método Simplex. Fuente: Elaboración propia
Como no quedan variables artificiales en la base (es decir, columna V.B. de la tabla) y el valor de la primera fila es cero se suprimen las columnas de las variables artificiales y se pasa a las fase 2 del método (en caso de que el valor sea diferente de cero, significa que el problema no tiene solución básica factible).
SEGUNDA FASE
En la segunda fase del método se suprimen las columnas de las variables artificiales y se sustituye la función objetivo por la función original
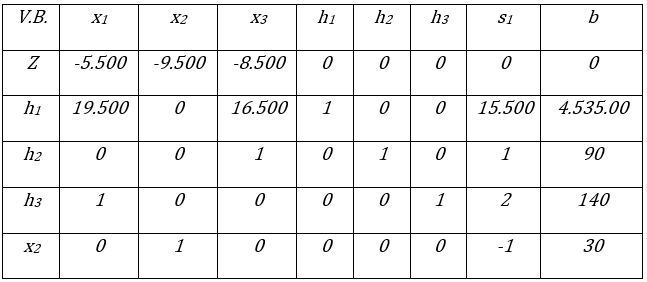
Tabla Inicial para la Segunda Fase del Método Simplex. Fuente: Elaboración propia
En la segunda fase la fila Z debe estar expresada en función de las variable básicas, es decir, el coeficiente de x2 debe ser cero, esto se logra sumando a la Fila 1 el producto de 9500 por la fila 5, lo cual se representa como F1+9500*F5
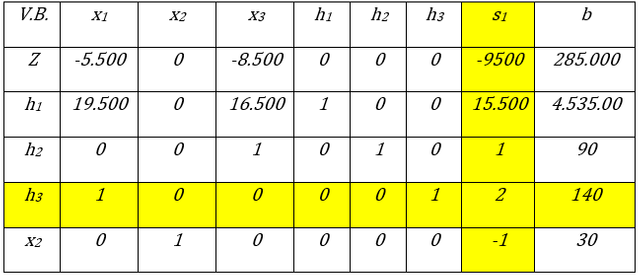
Iteración N° 0 de la segunda fase del Método Simplex. Fuente: Elaboración propia
Aplicando los criterios del método Simplex se obtiene:
Variable Entrante (VE): s1 Por ser el valor más negativo en los coeficientes de las variables (recuerde que se busca maximizar la función objetivo).
Variable Básica Saliente (VBS): h3 Debido a que la relación 140/2=70 es la menor (recuerde que los valores negativos se descartan).
La fila 3 se multiplica por ½ para que el elemento pivote (intersección entre la fila y columna seleccionadas sean cero) se convierta en 1, en las demás filas se convierten los elementos de la columna pivote en cero mediante las siguientes operaciones de fila:
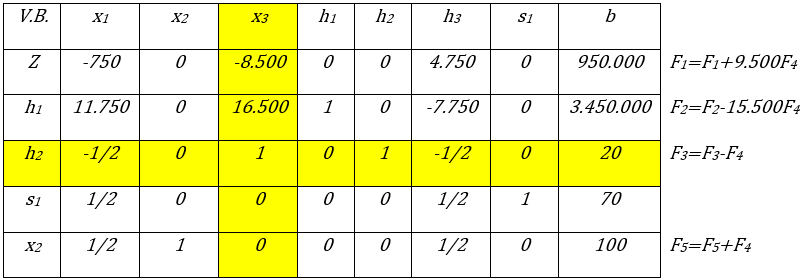
Iteración N° 1 de la segunda fase del Método Simplex. Fuente: Elaboración propia
Variable Entrante: x3 y Variable Básica Saliente: h2
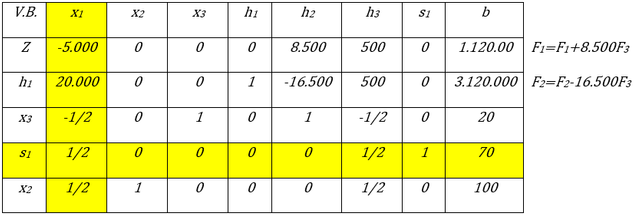
Iteración N° 2 de la segunda fase del Método Simplex. Fuente: Elaboración propia
Variable Entrante: x1 y Variable Básica Saliente: s1
La fila pivote se multiplica por 2 para convertir el elemento pivote en 1
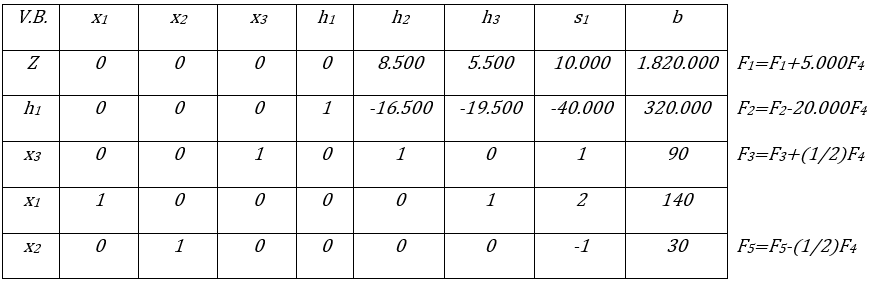
Iteración N° 3 de la segunda fase del Método Simplex. Fuente: Elaboración propia
Como todos los valores en la fila Z son positivos, la solución obtenida es óptima, es decir, los valores que maximizan la función objetivo son los siguientes:
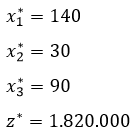
Lo cual para la señora Medina significa que si quiere maximizar sus ganancias debe preparar 140 hallacas de guiso tradicional, 30 de cochino y 90 de caraotas, obteniendo una ganancia total de Bs. 1.820.000, es decir, un 36,4% de su inversión original.
CONCLUSIONES
- Se puede observar que con añadir sólo una restricción de tipo >= la dificultad de resolver el modelo de programación lineal puede crecer de forma considerable.
- Es importante comprender el uso de las variables artificiales para las cuales su valor debe ser minimizado a cero en la primera fase del método simplex.
- Si la suma de las variables artificiales es mayor que cero entonces no existe Solución Básica Factible y se termina el proceso.
REFERENCIAS BIBLIOGRÁFICAS
González, Ysmael (2018) Aplicación del Método Simplex a un problema de maximización de ganancias fundamentado en los tópicos del Álgebra Lineal.
Taha, Hamdy A. (2012) Investigación de Operaciones 9° Edición. Editorial Pearson.


Amigo @ydavgonzalez, la matemática no es mi fuerte pero logre entender muy bien su explicación gran trabajo felicidades y éxitos...
Gracias por el apoyo, estimado @felixrodriguez.
Excelente la aplicación del modelado matemático para la resolución de un problema de la cotidianidad.saludos
Así es, estimado @joseleogon, gracias por el apoyo...
Saludos estimado amigo @ydavgonzalez, te comento que al leer el título me dio curiosidad, esto porque lo relacioné con la elaboración de Bioproductos sólidos, en agroecología algunos autores hacen uso de programación lineal para formular las mezclas de materiales orgánicos a degradar, en definitiva la matemática es una herramienta indispensable para optimizar e imitar ciertos eventos biológicos que ocurren en la naturaleza, y que bajo modelos matemáticos podemos replicar y de una u otra manera solventar problemas en nuestro caso de orden agrícola.
Saludos cordiales, sigamos creciendo.
Saludos @ydavgonzalez, me pareció genial el uso de ejemplos de la vida diaria para explicar la optimización lineal del transporte, mediante el método simplex; en tanto, ello implica que los modelos matemáticos tienen amplios usos y al relacionarlos con procesos cotidianos son más accesibles para el entendimiento de personas ajenas a esta especialidad.
Recordé unas cuantas cosas de mis estudios leyendo tu post. Tu el enunciado del ejemplo nº1 es tan detallado que parece real 😄 Saludos y éxitos.
También te invito a conocer y usar nuestra webapp oficial steemstem.io desde la cual puedes leer, publicar y comentar todas las publicaciones de la gran comunidad de #SteemSTEM y la subcomunidad #STEM-Espanol. Los artículos curados que hayan sido publicados desde esta webapp recibirán un 5% adicional del poder de voto.
Congratulations @ydavgonzalez! You received a personal award!
Thank you for taking part in the early access of Drugwars.
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard: