La hipocicloide.
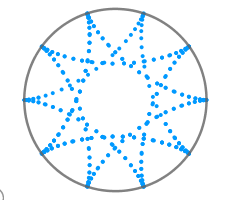
En mis dos post anteriores les hablé sobre la Cicloide y la Epicicloide, ahora para culminar con estas curvas les traigo la Hipocicloide otro tipo de ruleta cicloidal que de igual forma es la curva que describe un punto sobre una circunferencia generatriz, la cual como en el caso de la epicicloide rueda por una circunferencia directriz, siendo la diferencia que en este caso lo hace en la parte interna de esta, su nombre -Hipo- significa debajo y -ciclos- "círculo" es decir, debajo del círculo. Una curva hipocicloide es la trayectoria descrita por un punto sobre una circunferencia generatriz que rueda sin deslizar por el interior de otra circunferencia sin deslizamiento.
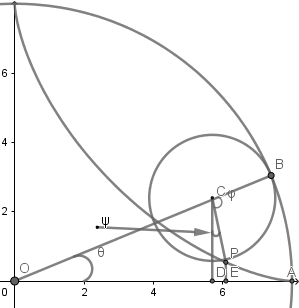
Siendo P(x,y) un punto cualquiera del lugar geométrico, r1 y r2 los radios de la circunferencia directriz y generatriz respectivamente; C el centro de la circunferencia generatriz, θ el ángulo que se forma por la recta que pasa por los centros y el semieje positivo x y A la posición inicial del punto P que describe la curva hipocicloide.
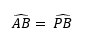
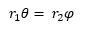
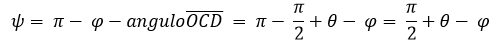
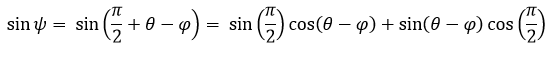
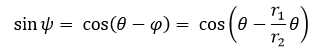
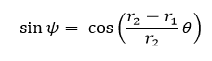
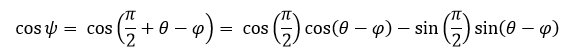
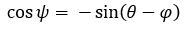
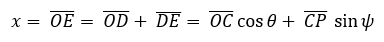(1) 
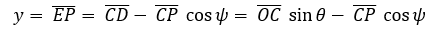(2)
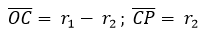
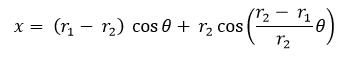
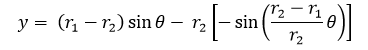
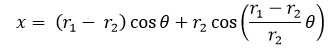
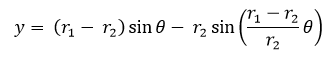
Sin embargo para desarrollar el tema con mayor comodidad más adelante, reescribiremos las ecuaciones de la siguiente forma:
;
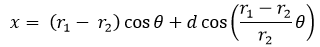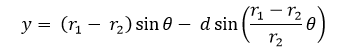
Siendo "d" la distancia respecto al centro de la circunferencia generatriz a la que estará ubicado el punto que describe la curva, anteriormente estaba situado a una distancia igual a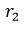 
, es decir, sobre la circunferencia generatriz siendo una hipocicloide normal.
La hipocicloide genera figuras muy interesantes la mayoría parecidas a estrellas, al igual que en la epicicloide estás figuras vienen dadas por el cociente "k" del radio de la circunferencia directriz y la generatriz, en el caso cuando k = 3 obtenemos un deltoide y en el caso k = 4 un astroide, las cuales son hipocicloides con tres y cuatro vértices respectivamente.
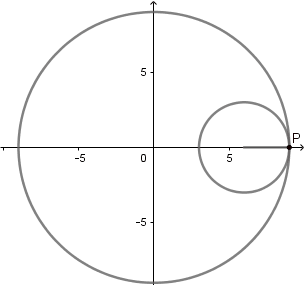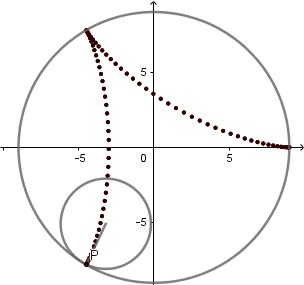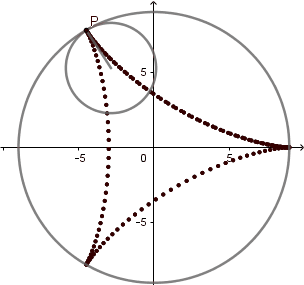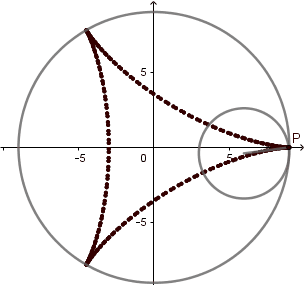
- La longitud de la curva es dieciséis veces el radio de la circunferencia generatriz. L = 16r
- El área interna de la curva es dos veces el área de la circunferencia generatriz. A = 2πr²
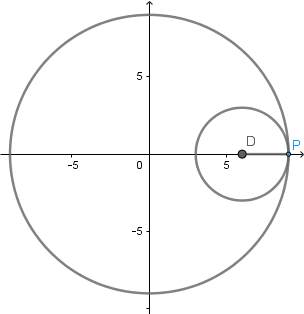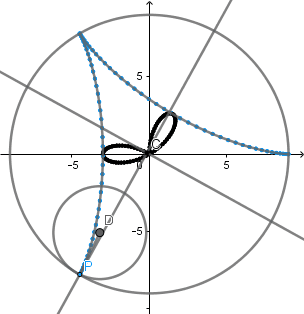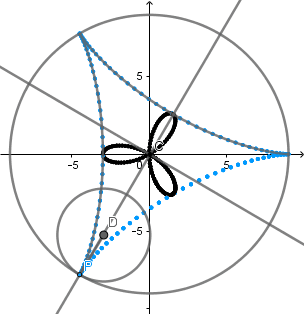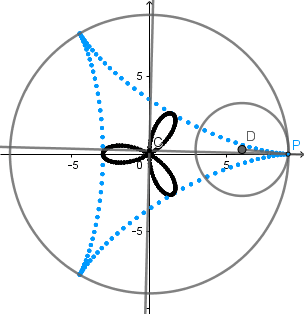
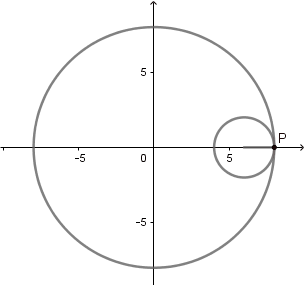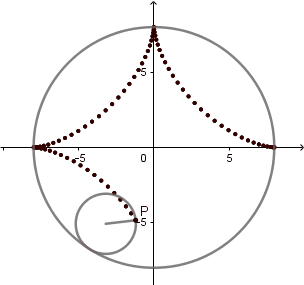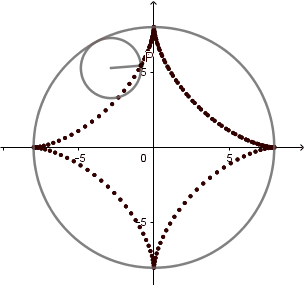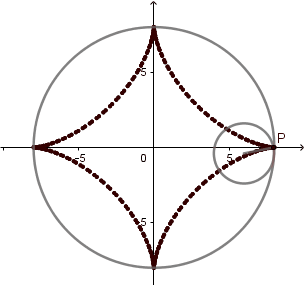
El 'astroide' del griego significa "estrella" esta curva tiene 4 vértices y comúnmente se genera cuando la circunferencia directriz es 4 veces el radio de la generatriz, sin embargo Daniel Bernoulli en 1725 consiguió otra forma de construir el astroide mediante hipocicloides y lo llamo doble generación del astroide y ocurre cuando k = 4/3.
Astroide doble generacion.
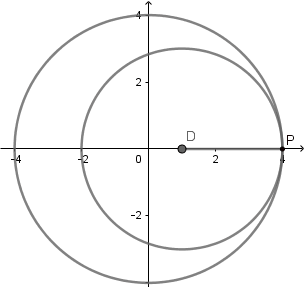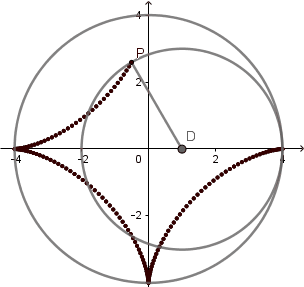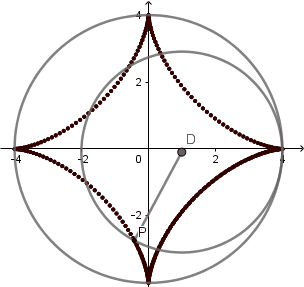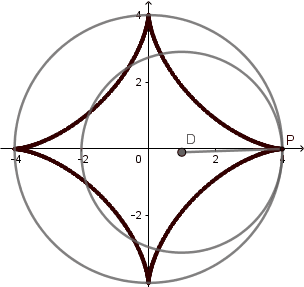
(GIF creado por mi usando el software matemático GeoGebra Classic 5).
- El astroide es una superelipse.
- La envolvente de una elipse resulta ser un astroide.
- La evoluta de un astroide es otro astroide.
- La podaria de un astroide es una "rosa de 4 pétalos".
De igual forma que con las curvas anteriores tenemos hipocicloides acortadas cuando el punto que describe la curva está dentro de la circunferencia generatriz y alargadas cuando el punto está fuera de la circunferencia generatriz.
Elipse como Hipocicloide acortada.
Si trazamos una hipocicloide acortada cuando el radio de la circunferencia directriz es dos veces el radio de la circunferencia generatriz r1 = 2.r2 y situamos el punto que describe la curva dentro de la circunferencia generatriz a una distancia de la mitad del radio de esta d = r2/2 obtenemos una elipse como resultado de una hipocicloide acortada.
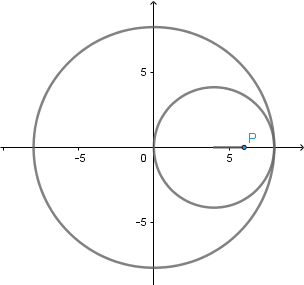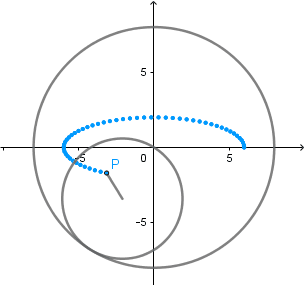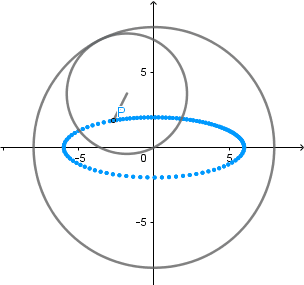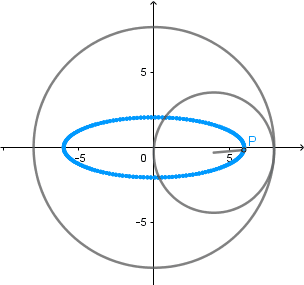
Elipse como Hipocicloide alargada.
De igual forma tomando como radio de la circunferencia directriz dos veces el radio de la circunferencia generatriz r1 = 2.r2 y situando el punto que describe la curva fuera de la circunferencia generatriz a una distancia de siete veces su radio d = 7.r2 obtenemos una elipse como resultado de una hipocicloide alargada.
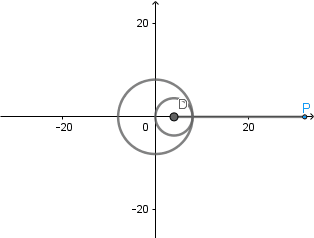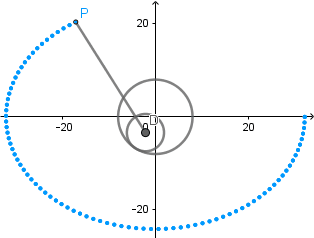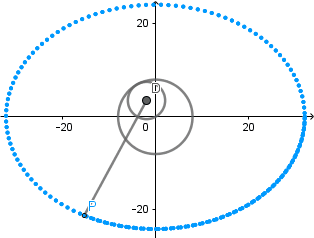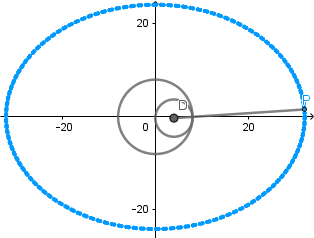
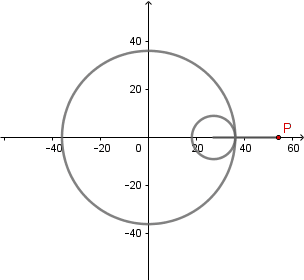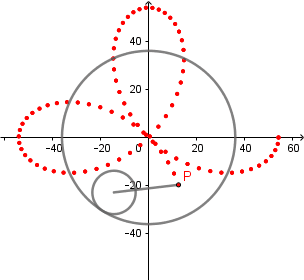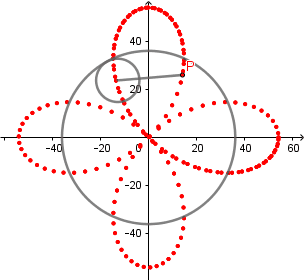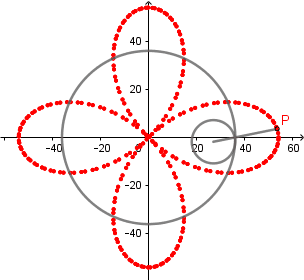
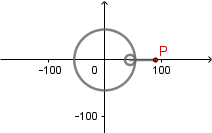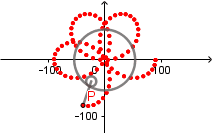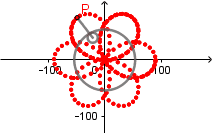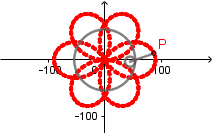
Rosa polar como hipocicloide alargada.
Rosa polar es el nombre que recibe una familia de curvas por la semejanza con una flor de pétalos, su ecuación viene dada por r(θ) = cos(kθ). La rosa polar se puede obtener como un caso particular de una hipocicloide alargada cuando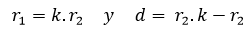 
el número de "pétalos" de la rosa viene determinado por el valor de k.
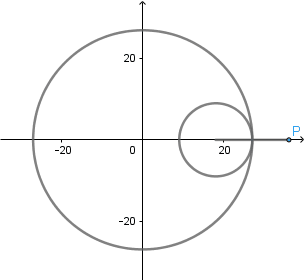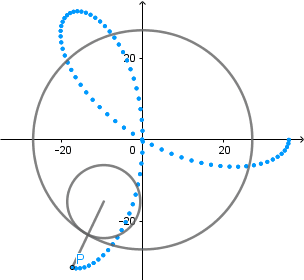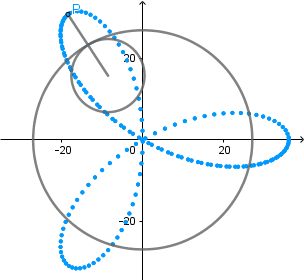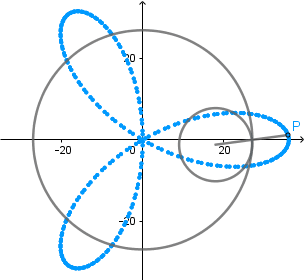
Espero hayan disfrutado de la interesante hipocicloide, si estan interesados en mas información pueden ingresar aqui para leer mi post anterior donde hablé sobre la epicicloide.
De Gante, C. Generación y Comparación de Patrones de Difracción de Aberturas Poligonales e Hipocicloides. Benemérita Universidad Autónoma De Puebla Facultad De Ciencias Físico Matemáticas. https://www.fcfm.buap.mx/assets/docs/docencia/tesis/fisica/2014/DeGanteGonzalezCesar.pdf
Corcho, F. (2017). La cicloide. Universidad de Sevilla Departamento de Geometría y Topología.
Rodriguez, R., Concepción, C. M. (2011). CURVAS MARAVILLOSAS. Facultad de matemática física y computación. http://dspace.uclv.edu.cu/bitstream/handle/123456789/9206/Trabajo%20de%20diploma%20%28Raydel%20y%20Cindy%29.pdf?sequence=1&isAllowed=y
Esta muy genial este post, dinámico y denso.
Gracias!! Un intento por conectar las matemáticas con la comunidad en general.
Tu publicación es una demostración visual donde se combina el tratamiento matemático y la aplicación inmediata de estas ecuaciones. Buen trabajo mi estimado @luiscd8a
Muchas gracias @iamphysical, aportando mi grano de arena para la comunidad #stem-espanol y steemit en general.